Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
Функция модуля y = |x|
Вступление
Сегодня мы рассмотрим функцию модуль x, узнаем все ее особенности и свойства, научимся строить график функции модуль х и находить значение функции модуль x. Поскольку мы уже прошли тему модуль, нам будет легко разобраться в терминологии, опираясь на наши знания. Итак, давайте разбираться со всем по порядку.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Функция y = |x|, ее свойства и график
В данной теме разберем график функции модуль x, а чтобы успешно научиться строить график данной функции, нужно помнить определение модуля числа.
Применив знания из темы “Модуль числа”, преобразуем данную нам функцию:
y={|abs|x|}{|=>|}y={|system.and|x, если x{|>=|}0;|-x, если x<0|}
Таким образом, график функции модуль x выглядит как две прямые: y = x при неотрицательных x и y= -x при отрицательных x.
Построим данные прямые по точкам:
y=x
y=-x
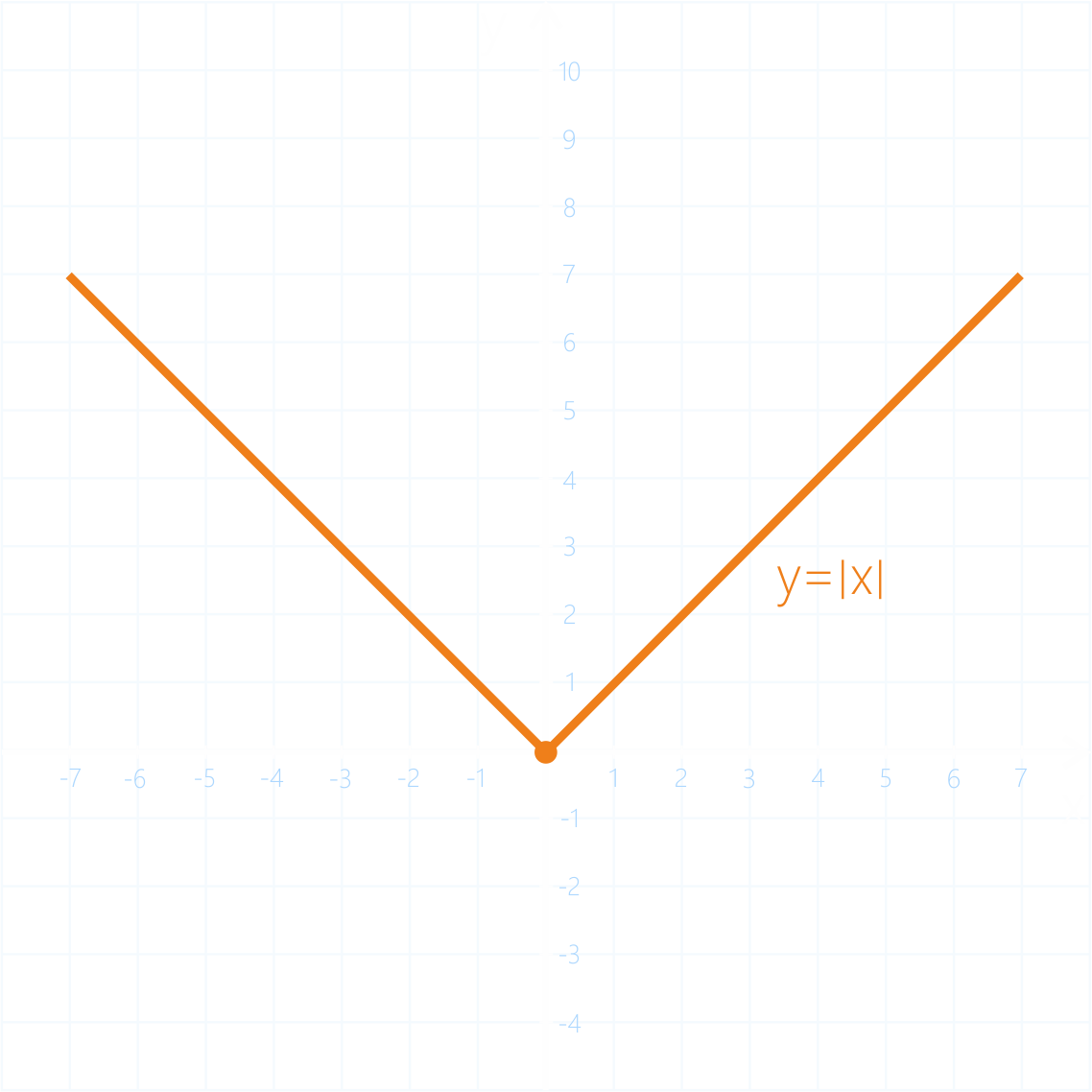
График с построенной функцией y = модуль х
Свойства функции y={|abs|x|}:
- Область определения функции: (-{|inf|};+{|inf|}), т.е. множество значений переменной x, для которых функция определена;
- Функция убывает при x: -{|inf|};0] и возрастает при x: [0;+{|inf|});
- Функция непрерывна, т.е. функция не имеет точек разрыва, другими словами, ее график представляет собой непрерывную линию;
- Область значений функции: [0; +), т.е. множество значений переменной y.
Заключение
Мы рассмотрели функцию модуль x, вспомнили, что такое модуль, узнали, как находить значение функции и строить график модуль х. Когда мы наглядно увидели очертание графика функции модуль x, то заметили, что свойства функции модуль х логично вытекают из картинки графика. Поэтому, чтобы их запомнить, достаточно внимательно посмотреть на изображение графика модуль x на координатной плоскости. Не нужно заучивать или зубрить свойства данной функции, их легко понять и обосновать, глядя на график. А сейчас давайте перейдем к заданиям от Виртуального Учителя. Они помогут нам освоить тему график функции модуль x, ее свойства и график. Нажимайте кнопку решать.
К вашей цели с Виртуальным учителем
