Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Функция y = tg(x). Свойства функции тангенса
Вступление
Мы приступаем к изучению новой функции - тенгенсоида - это график тангенса. Мы узнаем, как строить график тангенса, увидим его графическое изображение и детально его проанализируем. На основании наших выводов мы опишем все свойства графика тангенса. Этот алгоритм действий для нас уже хорошо известен. Именно так мы изучаем каждый график функции. Поэтому не будем терять время и приступим к изучению тангенсоиды.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Функция y = tg(x), её свойства и график
В данной теме рассмотрим, как выглядит график функции y = tg(x), а также разберем ее свойства.
Функция y = tg(x) имеет график:
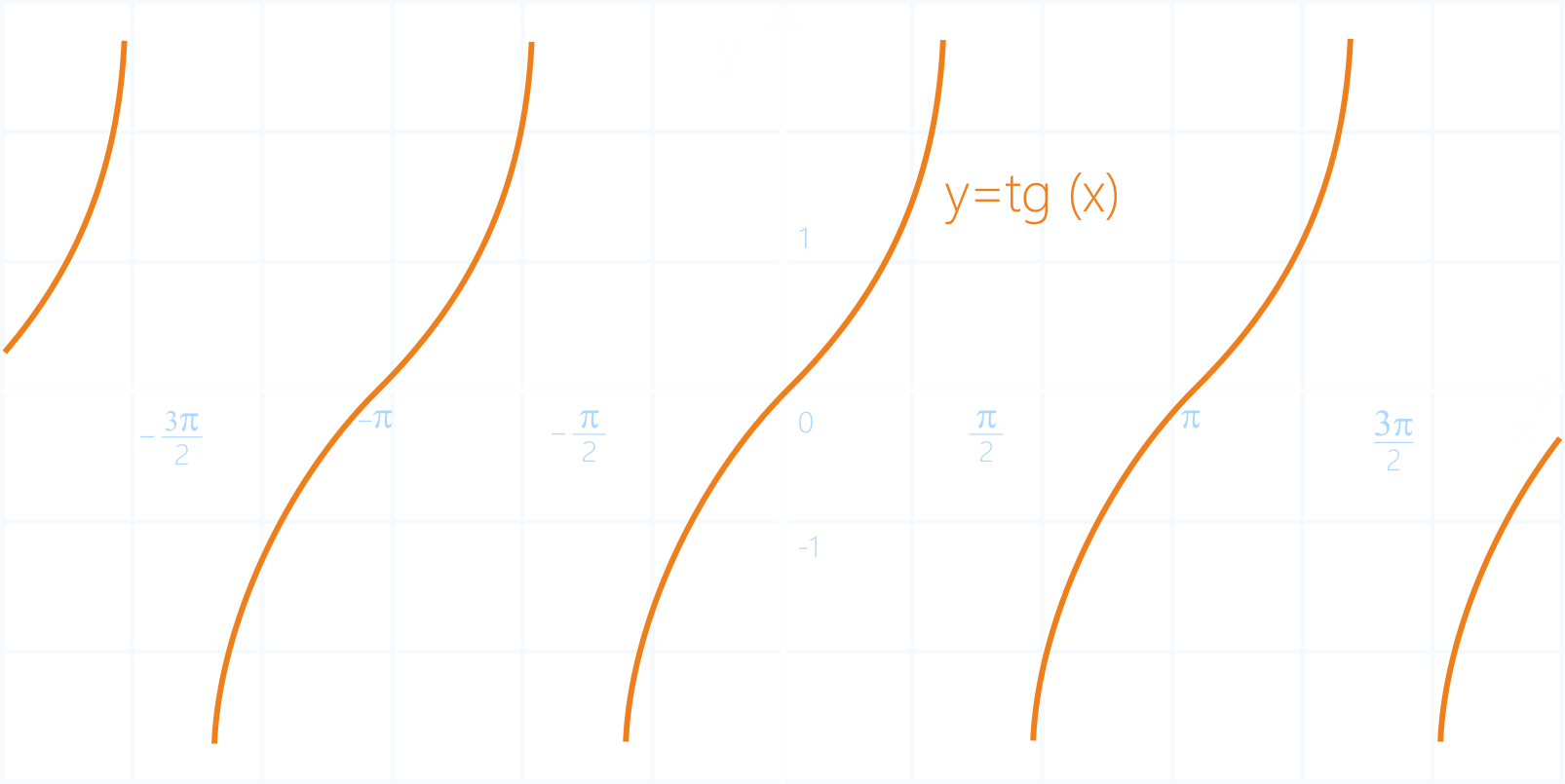
Полученный график тангенса называется тангенсоида. Заметим, что график тангенса в некоторых местах почти вертикален, это связано с тем, что {|tg|{|frac|{|pi|}|2|}|} не существует, т.к. при приближении угла x к {|frac|{|pi|}|2|}, значение {|cos|x|} становится всё ближе к нулю, и, соответственно, значение {|tg|x|} становится всё больше.
Свойства функции y={|tg|x|}:
- область определения функции - любое число, кроме {|frac|{|pi|}|2|}+{|pi|}n, где n - любое число,
- область значений функции - любое число,
- нечетная, т.к. {|tg|-x|}=-{|tg|x|},
- периодическая с периодом {|pi|},
- возрастает на [-{|frac|{|pi|}|2|}+{|pi|}n; {|frac|{|pi|}|2|}+{|pi|}n, n - любое целое число,
- максимальное значение: y{|index|max|} - не существует,
минимальное значение: y{|index|min|} - не существует, - y=0 при x={|pi|}n,
- имеет вертикальные асимптоты: x={|frac|{|pi|}|2|}+{|pi|}n.
Заключение
Сегодняшнее занятие мы посвятили изучению графика тангенса - тангенсоиде. Мы научились строить тангенсоиду, узнали, как выглядит данный график. Затем описали все восемь свойств тангенсоиды. Думаем, что Вы смогли убедиться в том, что описание свойств графика удобнее всего делать на основе его графического изображения. Именно оно наглядно подтверждает уместность приведения каждого из свойств. Для того чтобы закрепить пройденный материал, необходимо выполнить индивидуальные задания от Виртуального Учителя. Нажимайте кнопку решать и приступайте к подборке.
К вашей цели с Виртуальным учителем
