Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Определенный интеграл
Вступление
На одном из предыдущих занятий Вы узнали, что такое первообразная. Затем Вы поняли, что такое неопределённый интеграл. Мы можем его посчитать лишь с точностью до константы. Сегодня Вы познакомитесь с понятием определённого интеграла. Вы увидите, что такое криволинейная трапеция. Вы узнаете, что такое формула Ньютона-Лейбница, а также сможете понять, как интеграл связан с площадью криволинейной трапеции.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Определенный интеграл
Давайте вместе разберёмся с тем, что же такое определённый интеграл.
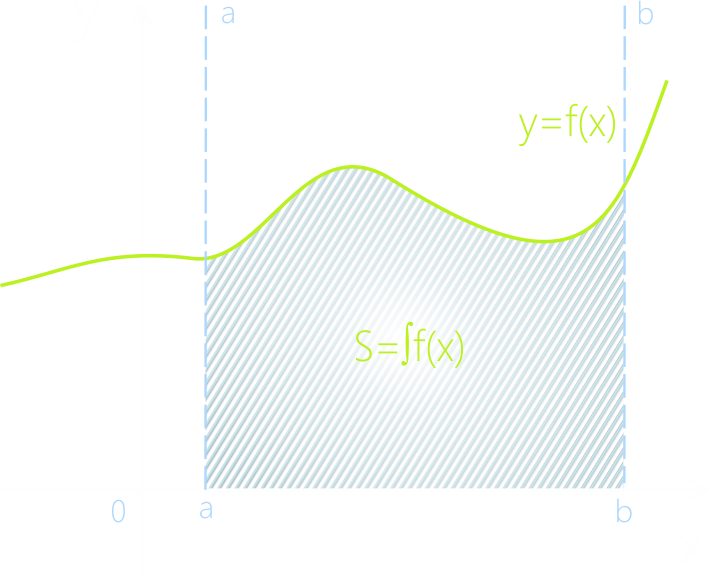
Определённый интеграл от a до b равен площади криволинейной трапеции.
Нарисуем функцию y=f(x).
Пусть она определена на отрезке [a;b]. Для простоты будем считать, что
функция f(x)>0 и неприрывна на отрезке .
Поставим себе задачу
найти площадь криволинейной трапеции, ограниченной прямой Ox, , и графиком непрерывной функции .
Разобъём отрезок [a;b] на n частей точками x{|index|0|},x{|index|1|},x{|index|2|}...x{|index|n-1|},x{|index|n|} так, чтобы удовлетворялось условие a=x{|index|0|}<x{|index|1|}<x{|index|2|}...<x{|index|i|}<x{|index|i+1|}...<x{|index|n-1|}<x{|index|n|}=b.
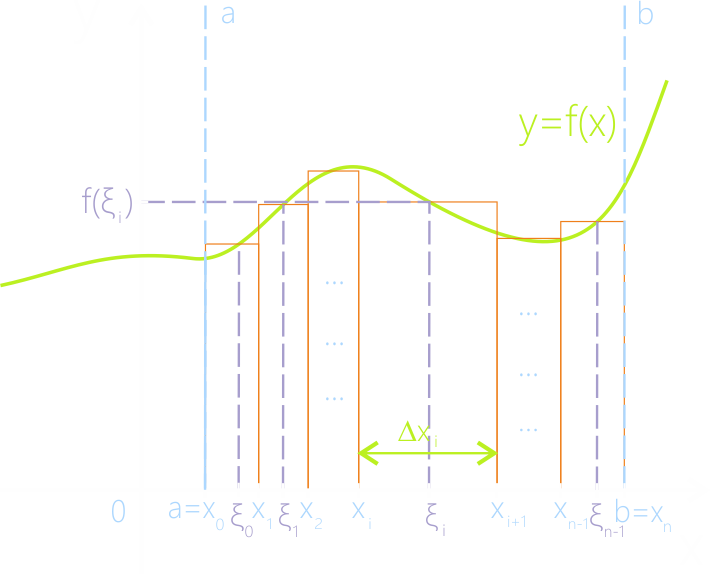
В итоге мы разбили
отрезок [a;b] на n частичных промежутков [x{|index|0|};x{|index|1|}],[x{|index|1|};x{|index|2|}], ... ,[x{|index|i|};x{|index|i+1|}], ...,[x{|index|n-1|};x{|index|n|}] с длинами △x{|index|0|}, △x{|index|1|}, ..., △x{|index|i|}, ..., △x{|index|n-1|} соответственно.
Отрезки не обязательно
одинаковые. Какие-то отрезки короче, какие-то длиннее.
В каждом из полученных промежутков
опять же произвольно выбираем точки ξ{|index|0|},ξ{|index|1|},ξ{|index|2|}, ..., ξ{|index|i|},...,ξ{|index|n-1|}.
Рассмотрим i-й промежуток [x{|index|i|};x{|index|i+1|}].
Его длина, очевидно, равна △x{|index|i|}=x{|index|i+1|}-x{|index|i|}.
Значению аргумента ξ{|index|i|} соответствует значение функции {|func|f|ξ{|index|i|}|}, и произведение {|func|f|ξ{|index|i|}|}*△x{|index|i|} в точности равно площади соответствующего
оранжевого прямоугольника.
Аналогично устроен каждый
отрезок.
Составим сумму, которая равна площади оранжевой ступенчатой фигуры: σ={|func|f|ξ{|index|0|}|}*△x{|index|0|}+{|func|f|ξ{|index|1|}|}*△x{|index|1|}+...{|func|+f|ξ{|index|i|}|}*△x{|index|i|}+...+{|func|f|ξ{|index|n-1|}|}*△x{|index|n-1|}.
Данная сумма называется интегральной
суммой.
Что означает прилагательное
«интегральной»? В широком смысле слова интегрировать – это значит, что-то объединять.
В данном случае интегральная сумма σ объединяет площади оранжевых прямоугольников
и с некоторой точностью приближается к площади криволинейной трапеции: σ?S
Теперь давайте задумаемся:
как улучшить точность приближения?
Немного подумав, становится очевидным,
что когда мы увеличиваем и увеличиваем значение n увеличивается и точность приближения. При этом
количество отрезков ,, ... ,, ..., растёт, а их длины – уменьшаются.
Количество точек тоже возрастает, и ступенчатая фигура всё больше
и больше становится похожа на криволинейную трапецию.
И, когда количество отрезков
разбиения устремить к бесконечности n{|=>|}{|inf|}, то интегральная сумма (площадь ступенчатой
фигуры) будет стремиться к площади криволинейной трапеции: σ{|=>|}S.
Таким образом, площадь криволинейной
трапеции равна пределу интегральной суммы при стремлении к нулю максимального
отрезка △x{|index|max|}: S={|lim|σ|△x{|index|max|}|0|}.
Теперь, осталось несколько шагов преобразования:
1) Если и, следовательно, △x{|index|max|}{|=>|}0, то значения {|func|f|ξ{|index|i|}|} стремятся «покрыть» все значения функции {|func|f|x|} из промежутка ,
то есть: {|func|f|ξ{|index|i|}|}{|=>|}{|func|f|x|}, при этом пределы интегрирования: {|dint|||a|b|}.
2) И, наконец, длина любого
промежуточного отрезка △x{|index|i|} становится бесконечно малой. Обозначение
этой бесконечно малой длины мы тоже хорошо знаем, оно указывает, что объединение
ведётся по переменной «икс»: d(x)
В результате площадь криволинейной
трапеции: S={|lim|σ|△x{|index|max|}|0|}={|dint|{|func|f|x|}|x|a|b|}.
Определение: конечный предел интегральной суммы {|func|f|ξ{|index|0|}|}*△x{|index|0|}+{|func|f|ξ{|index|1|}|}*△x{|index|1|}+... при , не зависящий ни от способа
дробления отрезка , ни от выбора точек ξ{|index|i|}, называется определённым интегралом
функции {|func|f|x|} по промежутку , и обозначается символом {|dint|{|func|f|x|}|x|a|b|}.
При этом функция {|func|f|x|} называется интегрируемой в промежутке .
Для интегрируемости (а, значит, существования
конечной площади), напоминаю, достаточно непрерывности функции на отрезке .
Но, при решении задач, такую формулу применять довольно сложно. Поэтому нашли побее простую формулу для поиска площади криволенейной трапеции (определённого интеграла).
Как Вы успели заметить в определении определённого интеграла: определённый интеграл не зависит от способа разбиения промежутка и от выбора точек . Важен только нижний и верхний предел интегрирования, а также сама функция {|func|f|x|}.
Для решения задач на поиск определённого интеграла функции была выведена более простая формула Ньютона-Лейбница:
{|dint|{|func|f|x|}|x|a|b|}=F(b)-F(a), где F(x) - первообразная функция для функции f(x). Заметим, что при вычитании константы сокращаются, поэтому мы сможем точно посчитать площадь под графиком от a до b.
Заключение
Вы уже знакомы с понятиями первообразной и интеграла. Сегодня Вы узнали, что такое определённый интеграл. Вы поняли, что такое криволинейная трапеция, а затем смогли найти её площадь. Эта площадь подсчитана точно, потому что константы первообразных уничтожаются. Поэтому такой интеграл называется определённым. Очень важно уметь находить площади фигур при интегрировании, сегодня Вы познакомились с формулой Ньютона-Лейбница. Это создатели интегрального и дифференциального исчисления.
К вашей цели с Виртуальным учителем
