Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Показательная функция
Вступление
Функция, которую мы с Вами сегодня изучим, имеет название показательная. Мы узнаем, какой вид у показательной функции, затем рассмотрим ограничения, которые она имеет, и знаем каковы причины данных ограничений. После этого мы построим график показательной функции и, опираясь на него, опишем свойства показательной функции. Давайте начинать.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Показательная функция y = a^x
Показательная функция - функция вида y=a{|pow|x|} (функция a в степени x), где a>0, a≠1.
Ограничения на основание степени возникли из-за того, что
- при a=1 функция принимает вид y=1{|pow|x|}{|=>|}y=1, а данная функция является линейной, аналогично при a=0,
- при a<0 степень с рациональным показателем не определена.
Построим график показательной функции, взяв, к примеру, a=3.
Строить будем по точкам, а после этого точки аккуратно соединим, чтобы получилась плавная линия.
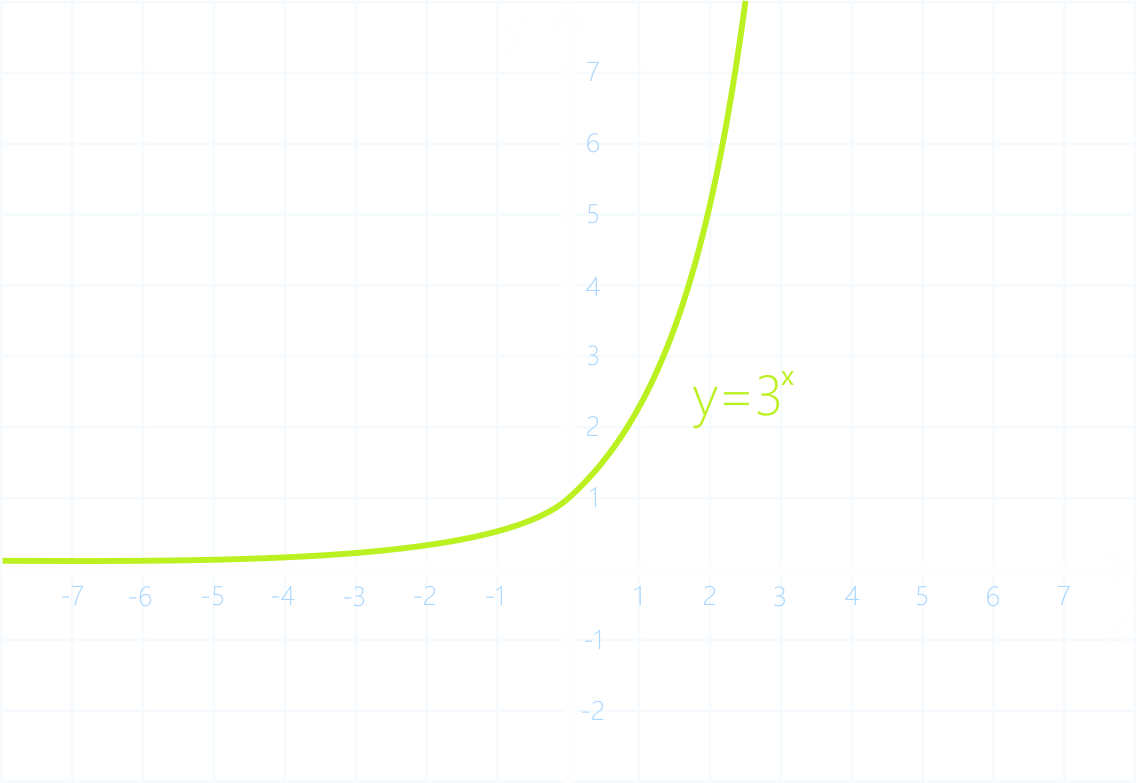
График показательной
функции
Заметим, что чем больше значение a, тем функция все ближе к оси ординат, другими словами, функция быстрей возрастает.
Свойства показательной функции y=a{|pow|x|} (функция a в степени x), где a>0, a≠1:
- определена на множестве всех действительных чисел,
- непрерывна на множестве всех действительных чисел,
- область значений функции - множество всех положительных чисел
- возрастающая
- ось абсцисс - асимптота графика функции.
Заключение
Итак, благодаря сегодняшнему занятию мы с Вами узнали много нового о показательной функции. Мы выучили её определение, узнали, какие ограничения имеет показательная функция. После чего мы построили график показательной функции и описали свойства показательной функции. Как и на предыдущих уроках, график стал для нас прекрасным наглядным пособием, с помощью которого легко определить и описать все свойства функции. А теперь давайте решим индивидуальные задания по теме показательная функция. Нажимайте кнопку решать и переходите к подборке.
0

Аккаунт
Учёба
Статистика
