Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Понятие движения. Свойства движения
Вступление
Слово движение Вы изучали на уроках математики в начальной школе. На уроках геометрии Вы познакомились с понятием вектора, отрезка, в котором указано направление
движения. На уроках физики также раскрывается тема движения. В геометрии
понятие движения тесно связано с симметрией. Задачи, связанные с движением
геометрических фигур, часто встречаются в заданиях ОГЭ и ЕГЭ. Поэтому
предлагаем приступить к изучению понятия движения в геометрии.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Понятие движения. Свойства движения
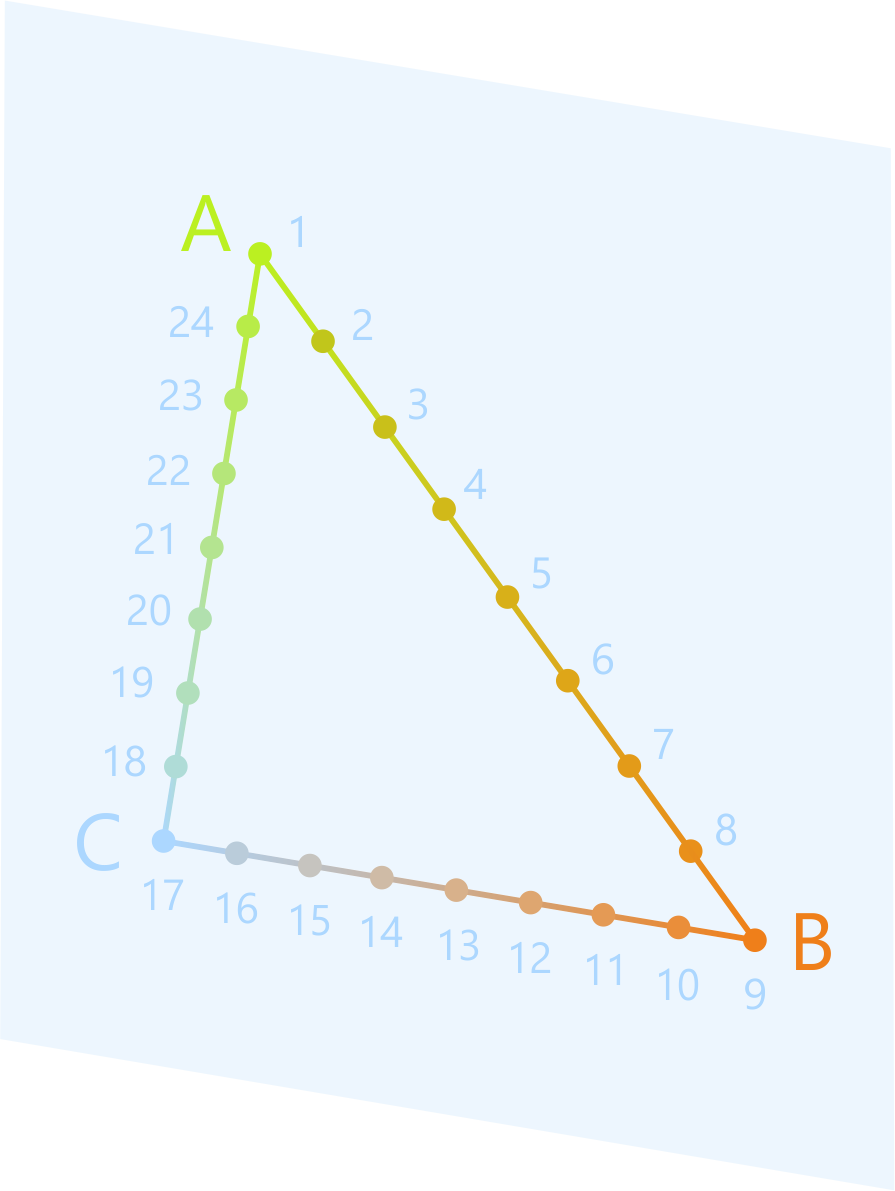
Рассмотрим
произвольный треугольник. На нём мы отметили 24 точки для наглядности, в
действительности же Вы понимаете, что точек намного больше.
Посмотрим, как будет происходить процесс
отображения плоскости на себя.
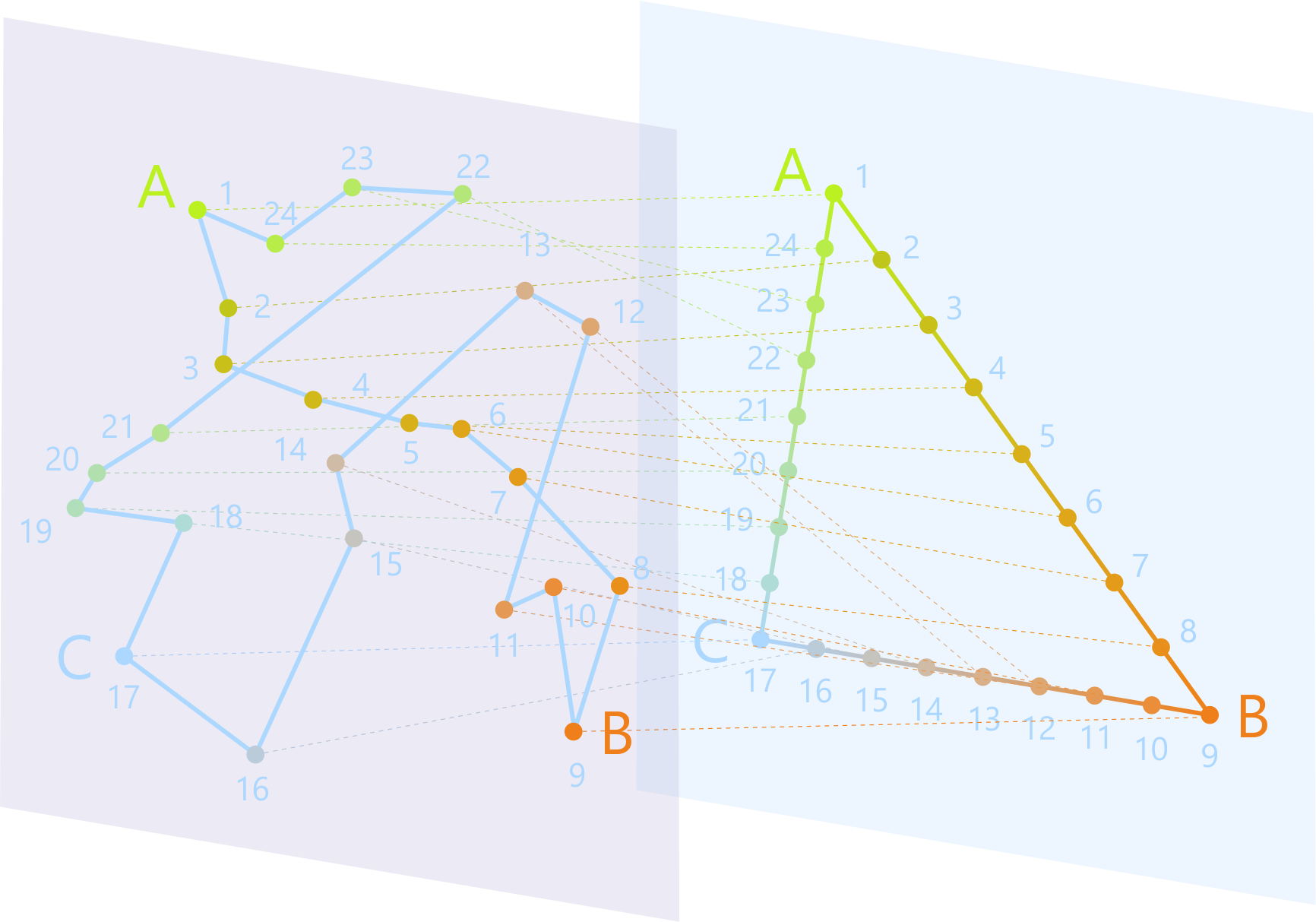
Если мы отобразим точки произвольно, то треугольника уже не получится,
что хорошо видно на рисунке. Это нельзя назвать движением треугольника.
Движением треугольника можно считать полное его отображение.
Рассмотрите рисунок.
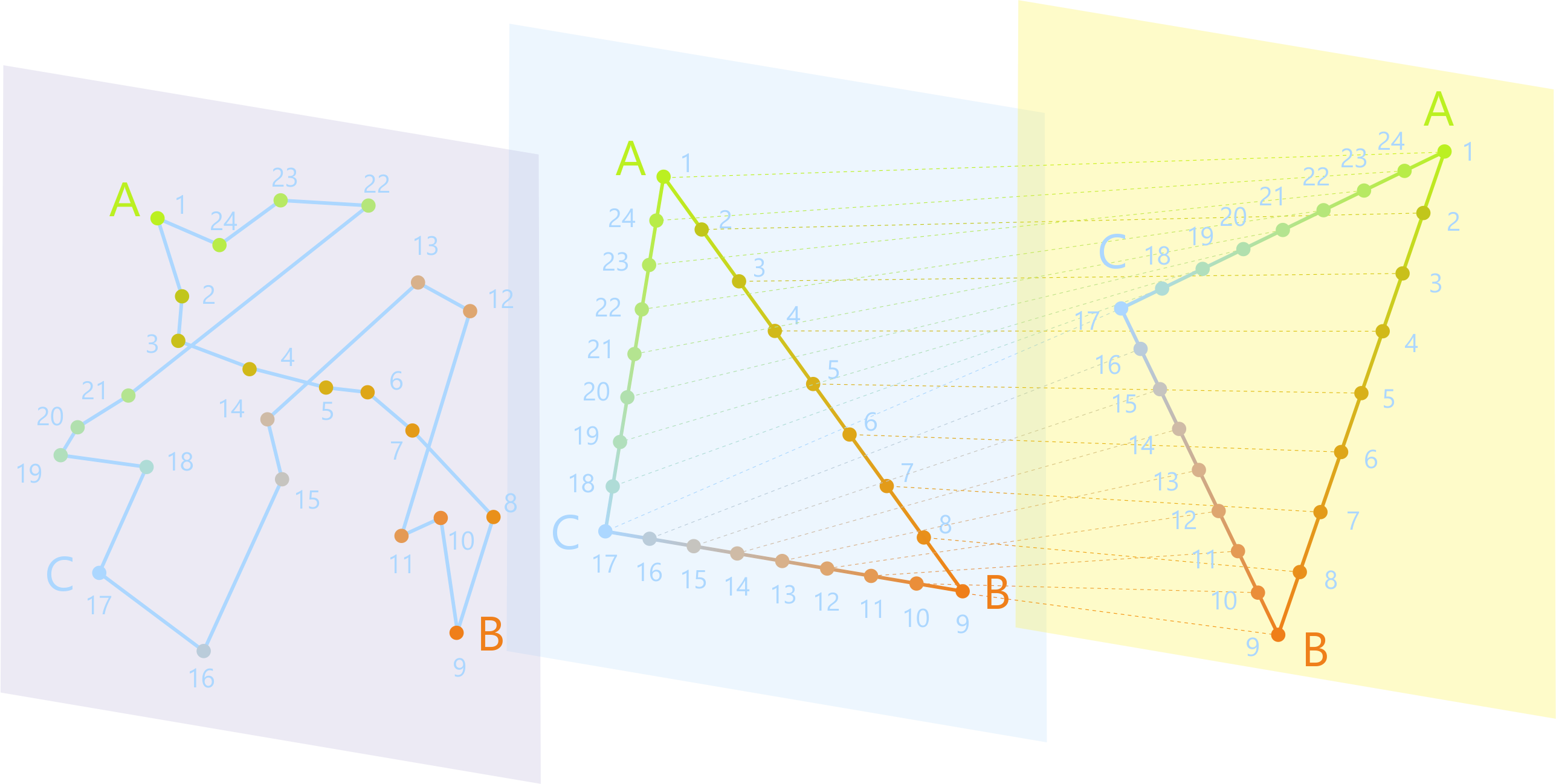
Таким образом можно перенести не только
треугольник, а любую произвольную фигуру, поэтому определение движения для
геометрии будет выглядеть так:
Движение в геометрии — процесс отображения плоскости на саму себя, при
котором сохраняется расстояние между двумя разными точками, выбранными
случайным образом.
Свойства движения можно сказать одной фразой:
При этом любая геометрическая фигура, будь то отрезок
или многоугольник, при движении сохраняет свой размер и форму.
Это значит, что при движении:
Сохраняется взаимное расположение. Если 3 точки лежали на одной прямой, то после переноса они переходят в 3 точки, которые лежат на одной прямой. При этом, точка, лежащая между двумя другими, переходит в точку, лежащую между образами двух других точек.
Сохранение углов. Все углы отображаются на угол такой же величины.
Сохранение площадей. Все фигуры при движении сохраняют свою форму и площадь.
Заключение
Движение
в геометрии тесно связано с понятием симметрии. Если представить плоскость как
бесконечный бумажный лист, то при его движении целостность листа сохраняется.
При этом лист можно сдвинуть в любом направлении, повернуть его или
перевернуть. Эти манипуляции означают разные виды движений, с которыми Вы
познакомитесь на следующих занятиях. А сейчас приступайте к решению
геометрических задач, чтобы лучше понять смысл движения с точки зрения
геометрии.
К вашей цели с Виртуальным учителем
