Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Возведение алгебраической дроби в степень
Вступление
Задания на нахождение степени частного будут регулярно встречаться на контрольных и проверочных работах. Деление степеней - это та тема, которую обязательно нужно выучить. И как мы уже знаем, наша задача - понять суть математических процессов. Именно это залог успешных и безошибочных решений. Механическое повторение не даст долгосрочных результатов. А вот если Вы поняли, откуда взялась та или иная формула, и разобрались в алгоритме решения, вот тогда долгосрочный результат гарантирован. Так мы сегодня разберём степень частного, вместе выведем формулу и выучим алгоритм решения. Давайте начинать.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Степень частного
Рассмотрим случай при делении степеней с одинаковым показателем.
Правило: деление степеней с одинаковым показателем равно степени с таким же показателем и основанием, равным частному оснований степени делимого и степени делителя.
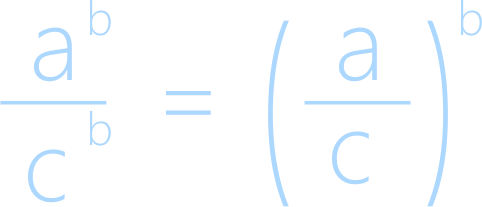
Другими словами, чтобы разделить степени с одинаковым показателем, необходимо разделить основания степеней, а показатель сохранить.
Это правило работает и в обратную сторону: степень частного равна частному степеней при одинаковых показателях степеней.
Данное правило можно легко доказать.
- Разложим числитель и знаменатель дроби на произведения одинаковых множителей.
- Представим дробь, как произведение нескольких одинаковых дробей вида: a : c.
- Преобразуем произведение одинаковых дробей в степень частного.
Таким образом и получится формула преобразования частного степеней в степень частного.
Заключение
Сегодня мы освоили методологию деления степеней. Для этого мы вывели формулу, подтвердили её, выучили правило нахождения частного степеней и рассмотрели пошаговое решение. Пора переходить к примерам на деление степеней, которые подготовил для Вас Виртуальный Учитель. Нажимайте кнопку решать и переходите к новым заданиям!
К вашей цели с Виртуальным учителем
