Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Аксиомы стереометрии
Вступление
Вы завершили изучение большого раздела геометрии - планиметрию. Все фигуры и их свойства мы рассматривали только на плоскости. Теперь мы с Вами приступаем к изучению стереометрии - нового раздела геометрии. В этом разделе мы будем рассматривать фигуры и их свойства не на плоскости, а в пространстве. Как Вы помните, в планиметрии изучение начиналось с аксиом, то есть утверждений, не требующих доказательства. И в стереометрии изучение начинается со знакомства с аксиомами стереометрии.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Аксиомы стереометрии
В стереометрии основные фигуры - точка, прямая, плоскость.
У плоскости нет определения, это базовое понятие, как прямая или точка. Плоскость можно представить неограниченной во все стороны.
Аксиомы:
- Через любые три точки, не лежащие на одной прямой, всегда проходит ровно одна плоскость.
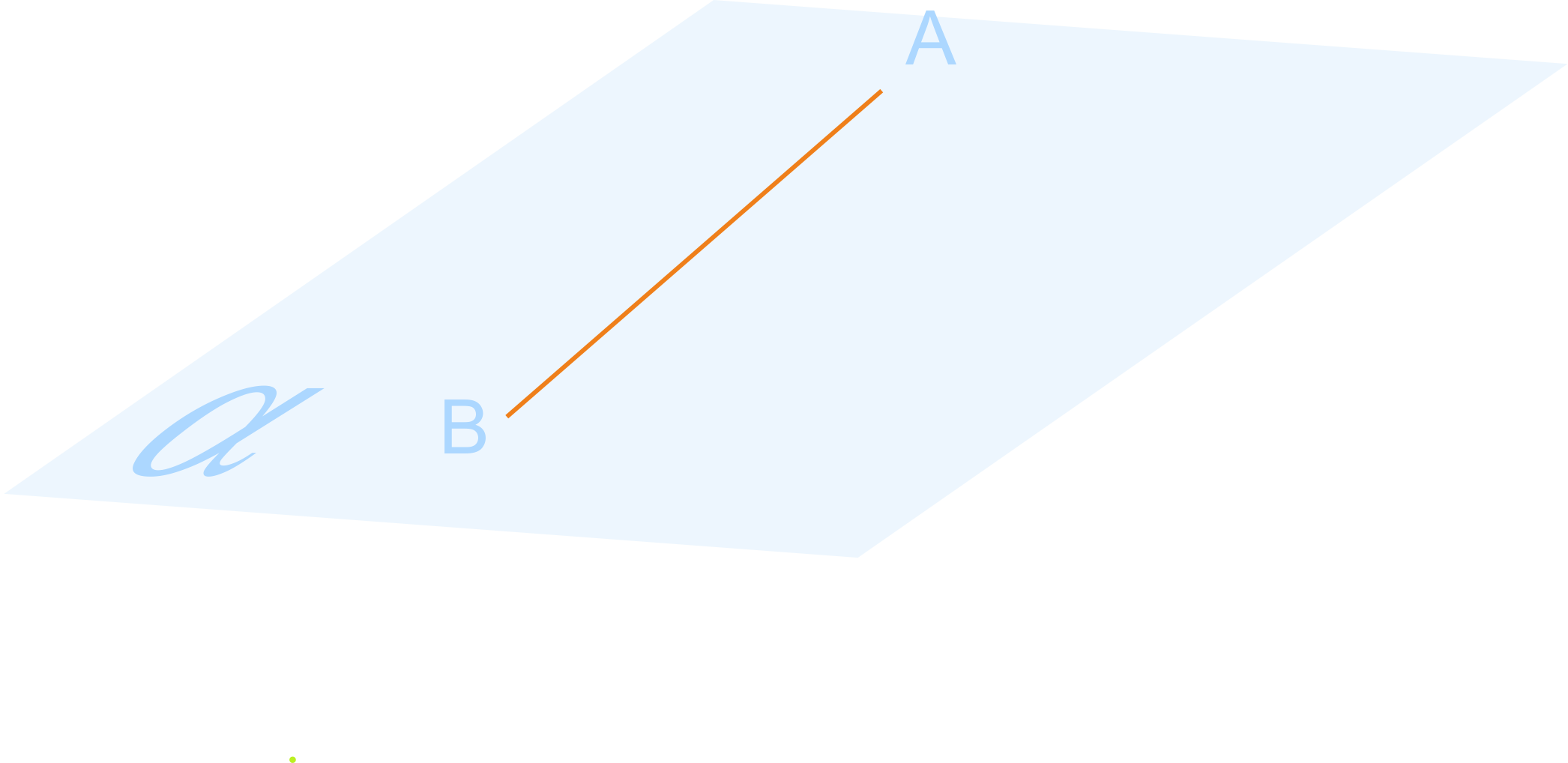
2. Если две точки принадлежат плоскости, то и прямая, проходящая через них, тоже ей принадлежит.
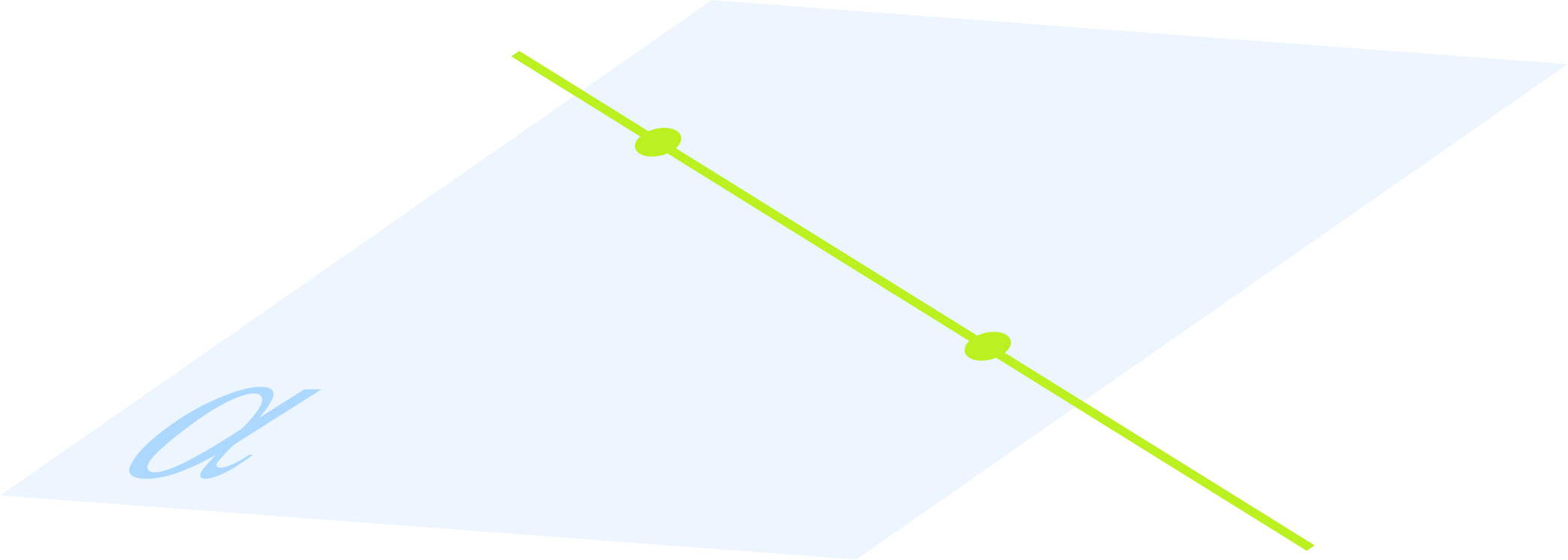
3. Если две плоскости имеют общую точку, то они пересекаются по прямой, содержащей все общие точки этих плоскостей.
Заключение
Мы приступили к новому разделу геометрии, к стереометрии. Теперь фигуры предстанут перед Вами не на плоскости, а в пространстве. Первый шаг в стереометрии - изучение аксиом, базовыми утверждениями, не требующими доказательства. Вы узнали три основные аксиомы стереометрии. На основании этих аксиом Вы будете в дальнейшем доказывать новые, всё более и более сложные утверждения.
К вашей цели с Виртуальным учителем
