Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Сравнение натуральных чисел
Вступление
В жизни часто используют сравнение чисел. Мы
сравниваем, какой товар дороже, а какой дешевле, куда ехать дальше, а куда
ближе, какой предмет тяжелее, а какой легче, какое событие состоится раньше, а
какое позже. При этом мы сравниваем числа, обозначающие цену, расстояние,
массу, время. Как происходит сравнение? Давайте разбираться.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме сравнение натуральных чисел
Сравнение натуральных чисел – это определение большего или
меньшего среди них. При записи в тетради для указания используют специальные
знаки: >(больше), <(меньше).
Записывают так:
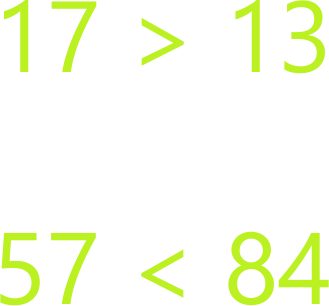
Сравнить небольшие числа просто. Мы знаем свойство
натурального ряда чисел и координатного луча:
Чем число ближе к началу, чем раньше оно называется при счете, тем оно
меньше. И наоборот, чем позже называют число при счете, чем оно дальше от
начала, тем оно больше.
Но как сравнить многозначные числа? Для этого мы не будем
считать до миллиона или чертить очень длинный координатный луч.
Воспользуемся знанием классов и разрядов.
Задание 1: Сравни числа 17 889 и 7 499.
Мы видим, что в первом числе в разряде десятков тысяч стоит цифра 1, а у
второго числа этого разряда нет.
Задание 2: Сравни числа 17 889 и
17 499.
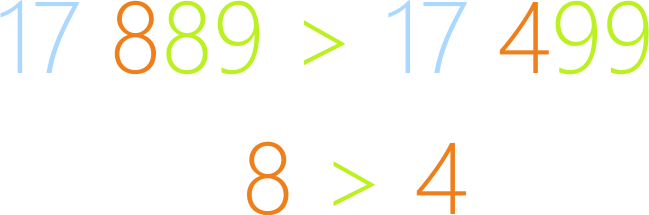
Мы видим, что у обоих чисел в классе тысяч одинаковое число –
17. Будем сравнивать разряды сотен: у первого числа 8 сотен (или 800), у
второго – 4 сотни (или 400). Делаем вывод:
Ответ: 17 889 > 7 499
Таким образом, выведем правило:
Сравнение используют в решении задач.
Например: Телевизор Самсунг стоит 17 889 рублей, а
телевизор Сони 17 499 рублей. Какой телевизор стоит дороже и на сколько?
Для решения задачи из большего числа вычитают меньшее, но
сначала нужно выяснить какое большее. Для этого и используют операцию
сравнения.
Как мы выяснили, 17 889 большее, тогда задачу решаем так:
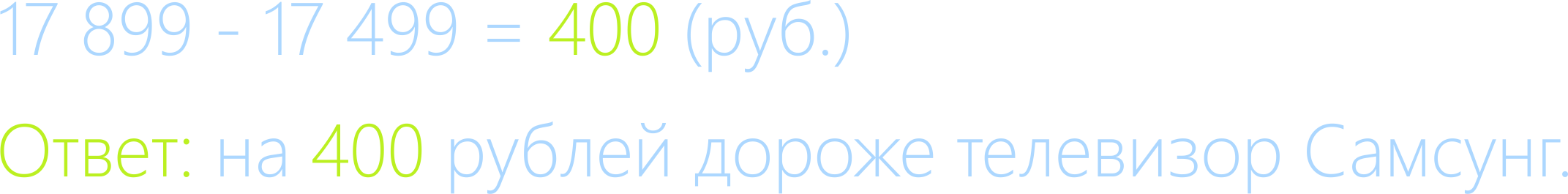
Сравнивать можно и три, и четыре и сколько угодно чисел.
Это делают, чтобы записать их в порядке возрастания (от меньшего
к большому) или убывания (от большого к меньшему).
Например, спортсмены прыгают в длину с разбега .
Вот их результаты:
Чтобы распределить спортсменов в рейтинге,
сравнивают результаты между собой. Получается так:
Операцию сравнения мы используем в жизни повсеместно: в
соревнованиях сравниваем результаты, при выборе покупок сравниваем цены и так
далее.
Заключение
Сравнение многозначных чисел – это определение
наибольшего или наименьшего, если чисел 2, и ранжирование чисел, если их 3 и
более. Существенно упрощает сравнение многозначных знание разрядов, так как
сравнивать начинают со старших разрядов.Тренируйтесь в сравнении натуральных
чисел, выполняя задания от Виртуального Учителя.
К вашей цели с Виртуальным учителем
