Деление на трехзначное число

Вступление

Теория по теме Деление на трёхзначное число

Сегодня мы рассмотрим деление на трёхзначное число. Такое деление выполняют письменно, оформляют в столбик. Давайте детальнее рассмотрим последовательность действий при таком делении.

Алгоритм несложен:

·        найти первое неполное делимое;

·        определить, сколько в частном цифр;

·        найти пробную цифру в частном;

·        умножить её на делитель;

·        найти остаток от деления;

·        сравнить остаток с делителем.

Если остаток меньше, снести следующую цифру  делимого и продолжить вычисления.

Если остаток больше, действие выполнено неверно, нужно подобрать другую пробную цифру.

Пример: 762 : 254 = ?

Найти первое неполное делимое: 72 – это очень мало, делить нужно 762, в частном одна цифра.

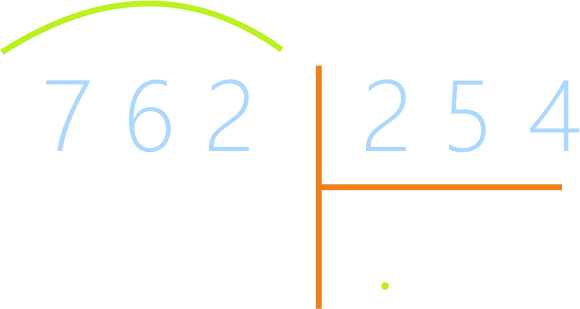
Для простоты деления делитель округляют и делят на 200. Так находят пробную цифру, для этого делят сотни на сотни:

7 : 2 = 3 (остаток 1)

3 – пробная цифра, ее проверяют, умножая на делитель 254.

254 * 3 = 762, деление закончено.

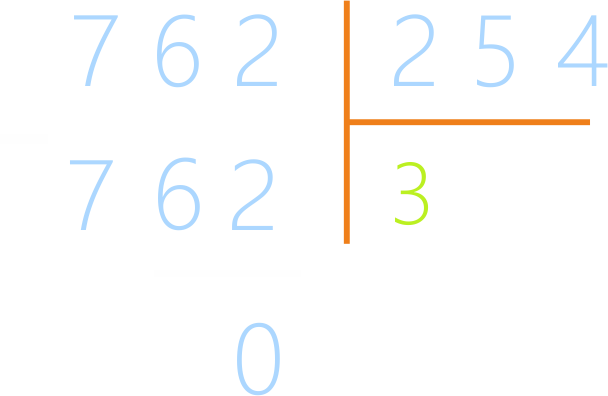
Если Вам дано задание решить пример на деление без остатка, а частное является однозначным числом, то можно применить ещё один полезный приём.

Пример: 762 : 254 = ?

Нужно сравнить последние цифры делимого 762 и делителя 254 и вспомнить, при умножении какого числа на 4 в конце произведения цифра 2.

3 * 4 = 12

8 * 4 = 32

Это пробные числа, умножьте их на делитель, и Вам станет понятно, какое из них подойдет.

В данном случае подойдет число 3, значит, частное 3, деление закончено.

Пример: 7 872 : 492 = ?

Сначала определяют первое неполное делимое, 78 меньше 492, значит, первое неполное делимое 782, в частном 2 цифры.

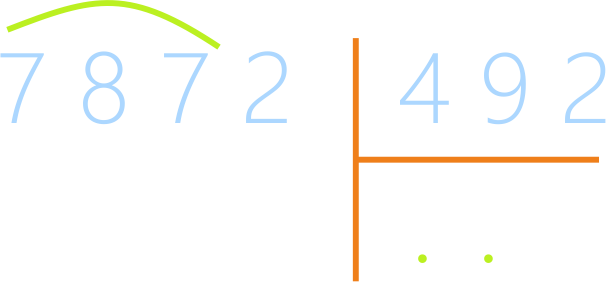
Если присмотреться, сразу станет понятно, что 492 – это почти 500, а, значит, первая цифра в частном – 1. Умножив 1 на 492 (делитель), Вы найдёте остаток.

Остаток от деления 295. Сравнение остатка с делителем: 295 < 492, значит, пробная цифра верна.

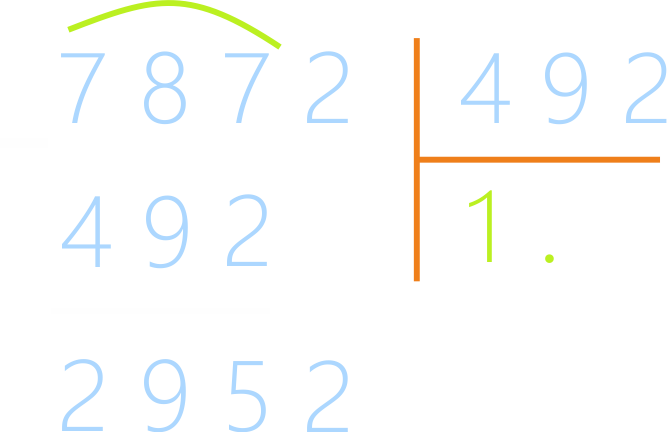
Далее сносят еще одну цифру из делимого и продолжают деление.

2952 – это почти 3000, 492 – это почти 500. Для удобства делят 30 сотен на 5 сотен. Пробная цифра – 6. Если умножить ее на 492 (делитель), можно понять, что результат подходит, остаток 0. Действие выполнено, результат 16.

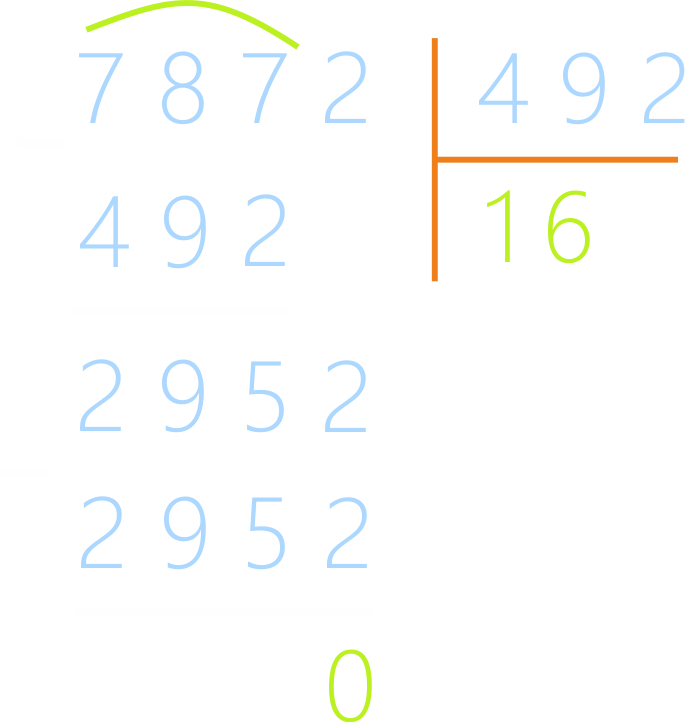
Заключение