Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Длина окружности
Вступление
Много тысячелетий ученые уделяли кругу особое внимание. Изучали его особенности и закономерности. Более 4 тысяч лет назад они заметили, что есть некое постоянное соотношение между длиной окружности и диаметром круга. Это соотношение сохраняется для окружностей любого размера! Какое это соотношение, смог рассчитать греческий учёный Архимед в III веке до н. э. Именно он определил точный диапазон нахождения числа Пи на числовой прямой и высчитал его значение 3,14. В наши дни точность числа Пи уже рассчитана до 22,4 трлн знаков после запятой! Но для школьных формул нам достаточно запомнить число Пи в виде 3,14. С соотношением определились, а что ещё нам необходимо знать, чтобы рассчитать длину окружности? Давайте разбираться.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Длина окружности
Для начала вспомним, что у окружности есть длина и радиус. Зная величину радиуса, можно определить длину окружности.
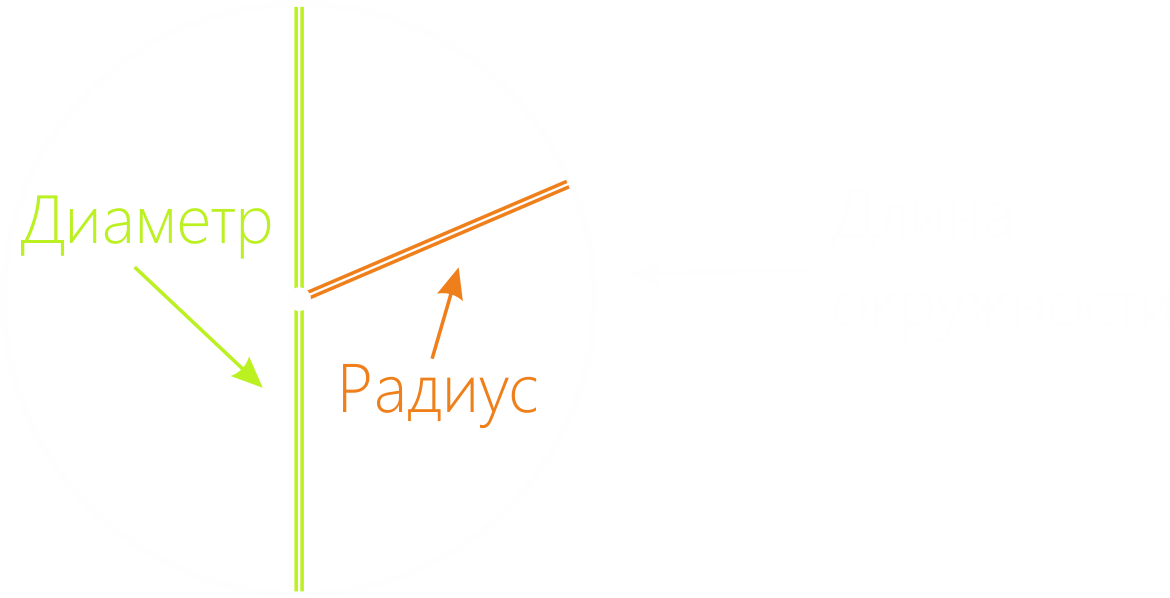
Окружность, её радиус и диаметр
Прежде чем написать формулу длины окружности, необходимо ввести новое число.
Число пи - это отношение длины окружности к ее диаметру.
Число пи обозначается греческой буквой π.
Численно число пи имеет бесконечное количество знаков после запятой, однако несколько первых цифр стоит запомнить.
π=3,1415926...
Чаще всего число пи записывают как 3,14.
Длина окружности равна удвоенному произведению числа π на ее радиус:
l=2*π*r, где r - радиус окружности.
Понятно, что раз число пи имеет бесконечное количество знаков после запятой, вычислить точную длину окружности невозможно, поэтому мы всегда вычисляем примерное значение.
Получается, что длина окружности равна произведению: 2*3,14*r
Так как диаметр окружности равен удвоенному радиусу, то формулу длины окружности можно переписать немного по-другому.
Длина окружности равна произведению числа π на ее диаметр:
l=π*d, где d - диаметр окружности.
Заключение
Итак, мы узнали, что длина окружности и её диаметр взаимосвязаны. Это соотношение сохраняется для всех без исключения окружностей. И для всех оно стабильно. Его величина названа числом Пи и равна 3,14. Мы узнали, как находить длину окружности, какие существуют для нахождения длины окружности. Прорешали разные виды задач с разными вводными данными. Давайте закрепим на практике пройденный материал. Виртуальный Учитель подготовил только самые необходимые для этого задания. Нажимайте скорее решать!
0

Аккаунт
Учёба
Статистика
