Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Формула суммы членов конечной геометрической прогрессии
Вступление
Древние мудрецы изучали числа. Понять, как числа взаимодействуют между собой, как выстраиваются в последовательности, какие свойства при этом обретают - всё это было сродни постижению тайн вселенной. Конечно, спустя тысячелетия, человечество нашло множество формул, которые описывают практически все взаимодействия чисел, в том числе и в геометрической прогрессии. Но корни этих знаний уходят глубоко в историю. Сегодня мы изучим одну из формул - формулу суммы членов геометрической прогрессии и научимся её применять.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Сумма членов геометрической прогрессии
В данной теме рассмотрим, как найти сумму членов конечной геометрической прогрессии.
Пусть дана прогрессия:
b{|index|1|}, b{|index|2|}, b{|index|3|}, b{|index|4|}, ... , b{|index|n-3|}, b{|index|n-2|}, b{|index|n-1|}, b{|index|n|}.
где:
b{|index|2|}=q*b{|index|1|}, b{|index|3|}=q*b{|index|2|}, ... ,b{|index|n|}=q*b{|index|n-1|}.
S{|index|n|} - сумма членов геометрической прогрессии.
S{|index|n|}=b{|index|1|}+b{|index|2|}+b{|index|3|}+b{|index|4|}+ ... +b{|index|n-2|}+b{|index|n-1|}+b{|index|n|}.
Чтобы найти сумму первых n членов геометрической прогрессии (при q≠1) воспользуемся формулой:
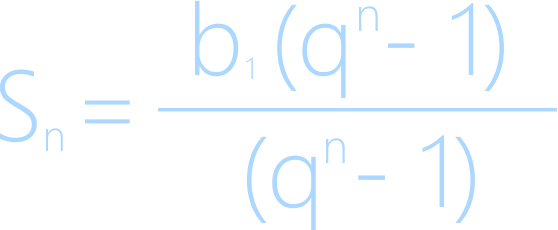
Формула суммы первых членов геометрической прогрессии
Таким образом, сумма геометрической прогрессии вычисляется по данной формуле, в которой число n - количество первых членов прогрессии, сумму которых необходимо вычислить.
Заключение
Итак, геометрическая прогрессия нами изучена. После сегодняшнего занятия Вы легко сможете находить сумму членов геометрической прогрессии с помощью формулы, которую мы изучили. Напомним, что любая теоретическая информация гораздо лучше запоминается, если закрепить её на практике. Именно для этого Виртуальный Учитель подготовил задания на нахождение суммы членов геометрической прогрессии. Эти задания уже ждут Вас. Нажимайте кнопку решать и приступайте к практике.
К вашей цели с Виртуальным учителем
