Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
Функция y = sin(x). График функции синуса
Вступление
Сегодняшнее занятие мы посвятим изучению синусоиды - графика функции синус. Мы узнаем, как строить данный график, увидим графическое изображение синусоиды. Затем опираясь на график синуса детально опишем все свойства синусоиды. После прохождения теоретической части нашего занятия мы перейдём к выполнению заданий и построению графика синусоиды. Давайте начинать.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Функция y = sin(x), её свойства и график
В данной теме рассмотрим, как выглядит график функции y = sin(x), а также разберем ее свойства.
Функция y = sin(x) имеет график:
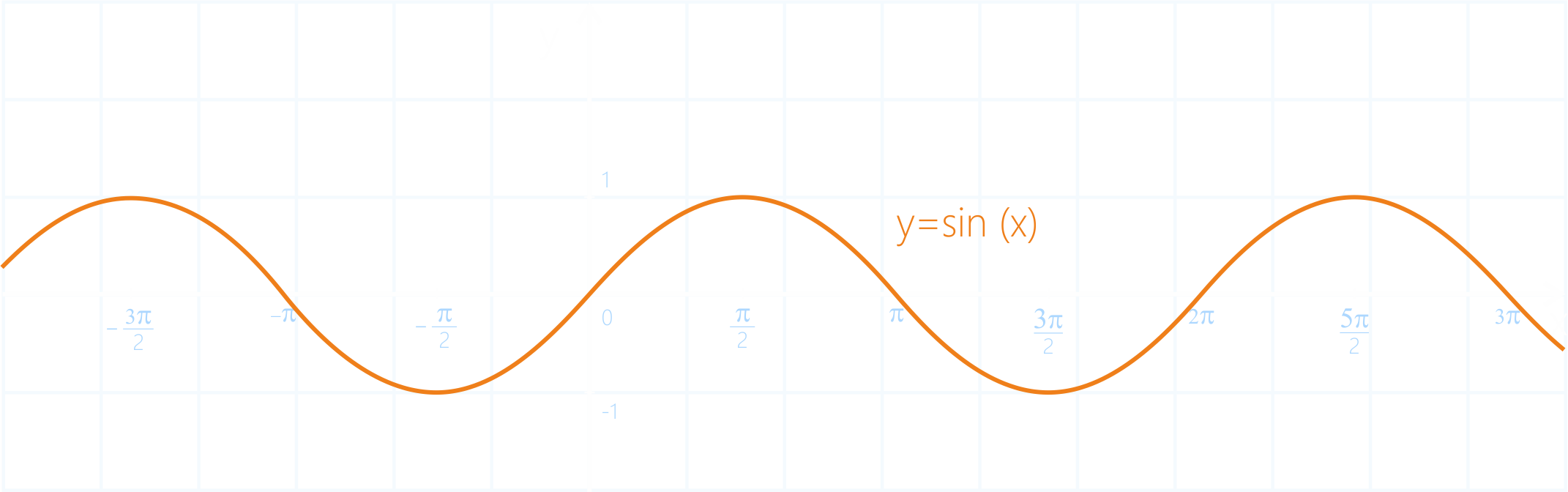
Полученный график синуса называется синусоида. Заметим, что данная функция периодическая, т.к. ее график бесконечно повторяется.
Свойства функции y={|sin|x|}:
- область определения функции - любое число,
- область значений функции: [-1;1],
- нечетная, т.к. {|sin|-x|}=-{|sin|x|},
- периодическая с периодом 2{|pi|},
- возрастает на [-{|frac|{|pi|}|2|}+2{|pi|}n;{|frac|{|pi|}|2|}+2{|pi|}n], n - любое целое число,
убывает на [{|frac|{|pi|}|2|}+2{|pi|}n;{|frac|3{|pi|}|2|}+2{|pi|}n], n - любое целое число,
- максимальное значение: y{|index|max|}=1 при x={|frac|{|pi|}|2|}+2{|pi|}n, n - любое число,
минимальное значение: y{|index|min|}=-1 при x=-{|frac|{|pi|}|2|}+2{|pi|}n, n - любое число, - y=0 при x={|pi|}n.
В свойствах синусоиды можно наглядно убедиться, посмотрев на график функции синуса.
Заключение
Сегодня мы с Вами изучили синусоиду - график функции синус. Как видите, в её построении нет сложностей. Это периодическая функция, график которой повторяется бесконечно. Именно на основе этого графика синуса мы сделали описание всех семи свойств синусоиды. Внимательно изучите эти свойства, они Вам ещё не раз пригодятся при решении задач. Чтобы лучше освоить тему синусоида решите индивидуальные задания, которые подготовил для Вас Виртуальный Учитель. Нажимайте кнопку решать.
0

