Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Конус. Площадь поверхности конуса.
Вступление
Недавно Вы познакомились с геометрическим телом, которое называется цилиндр. Давайте рассмотрим ещё одну пространственную фигуру – конус. На занятии Вы узнаете, что такое вершина конуса, основание конуса, образующая конуса и ось конуса. Вы познакомитесь с тем, чему равна высота конуса и как образуется боковая поверхность конуса. Вы увидите, что представляет собой развёртка конуса и чему равна её площадь. Вы научитесь находить площадь боковой поверхности конуса и площадь поверхности конуса.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Площадь поверхности конуса
Рассмотрим плоскость α и лежащую в этой плоскости окружность ω с центром в точке O и радиусом 𝑟. Рассмотрим точку 𝑃, лежащую вне плоскости α. Проведём через точку P и через каждую точку окружности ω прямые.
Тело, ограниченное такими прямыми и кругом с границей ω, называется конусом.
Каждый отрезок такой прямой, заключённый между точкой 𝑃 и точкой окружности – это образующая конуса.
Образованная ими поверхность – это боковая поверхность конуса.
Круг с границами ω представляет собой основание конуса.
Точка 𝑃 – это вершина конуса.
Радиус конуса – это радиус основания конуса.
Высота конуса равна длине его оси.
Ось конуса – это прямая 𝑂𝑃, проходящая через центр основания конуса и вершину конуса.
На рисунке показано, как образуется конус и обозначены основание конуса, образующая конуса, боковая поверхность конуса, вершина конуса и его ось.
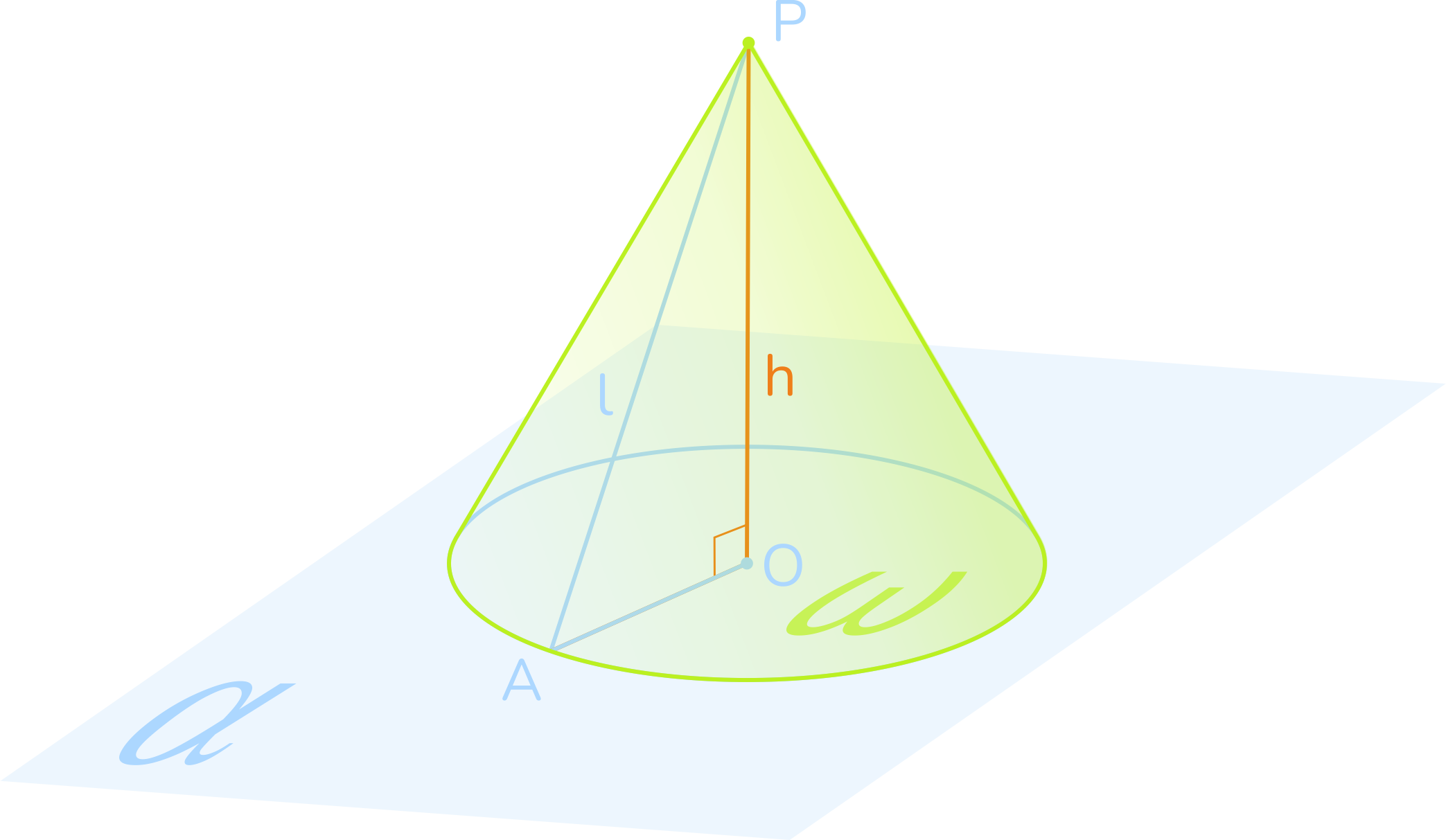
Рассмотрим, как найти площадь поверхности конуса. Представим, что боковую часть конуса разрезали по некоторой его образующей 𝑃𝐴. Тогда мы получим круговой сектор с центром 𝑃 и радиусом 𝑟, равным радиусу основания конуса. Такой круговой сектор называют развёрткой боковой поверхности конуса. Вначале найдём его площадь, это будет являться площадью боковой поверхности конуса. Пусть длина образующей конуса равна 𝑙, а градусная мера развёртки боковой поверхности конуса равна 𝛼. Тогда по формуле площади кругового сектора получаем:
S{|index|бок|}={|frac|πl{|pow|2|}|α|}
Найдём, чему равна градусная мера угла α. Длина кругового сектора боковой развёртки конуса равна длина основания конуса и равна 2πr. В то же время по формуле длины дуги она равна{|frac|πlα|180°|}. Получаем уравнение {|frac|πlα|180°|}=2πr, откуда α={|frac|360°r|l|}. Тогда:
S{|index|бок|}={|frac|πl{|pow|2|}|360°|}α={|frac|πl{|pow|2|}|360°|}*{|frac|360°r|l|}=πrl
Площадь основания конуса равна S{|index|окр|}=πr{|pow|2|}. Площадь поверхности конуса равна сумме площади боковой поверхности конуса и площади его основания: S{|index|кон|}=S{|index|бок|}+S{|index|осн|}= πrl+πr{|pow|2 |}=πr(r+l)
Заключение
Итак, Вы познакомились с новым геометрическим телом в пространстве. Теперь Вы знаете, что такое конус. В процессе занятия Вы научились определять, что такое основание конуса, образующая конуса, вершина конуса и ось конуса. Вы узнали, как образуется боковая поверхность конуса, чему равна высота конуса и его радиус. Вы узнали, как получается развёртка боковой поверхности конуса, как найти её градусную меру и площадь и как найти площадь поверхности конуса. Приступайте к выполнению заданий и тренируйте новые навыки.
К вашей цели с Виртуальным учителем
