Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Многоугольники. Равные фигуры
Вступление
Геометрические
фигуры окружают нас в жизни. Мы говорим, что тарелка похожа на круг, картина –
на квадрат или прямоугольник, праздничный колпак – на треугольник. В математике
каждая геометрическая фигура имеет свое название. Отличаются они между собой
количеством сторон, вершин, углов. При этом раньше Вы были знакомы лишь с
несколькими из них. Сейчас Вы cможете узнать, какие бывают геометрические
фигуры, и как их сравнивать.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Многоугольники. Равные фигуры
Вспомним понятие ломаной линии.
Ломаная линия – это 2 и более отрезков,
последовательно соединенных друг с другом концами.
На рисунке ломаная линия из четырех отрезков, то есть из
четырех звеньев.

Начертим ломаную линию из четырех звеньев, но замкнутую,
когда начало первого звена и конец последнего соединены.
Возьмем для примера:
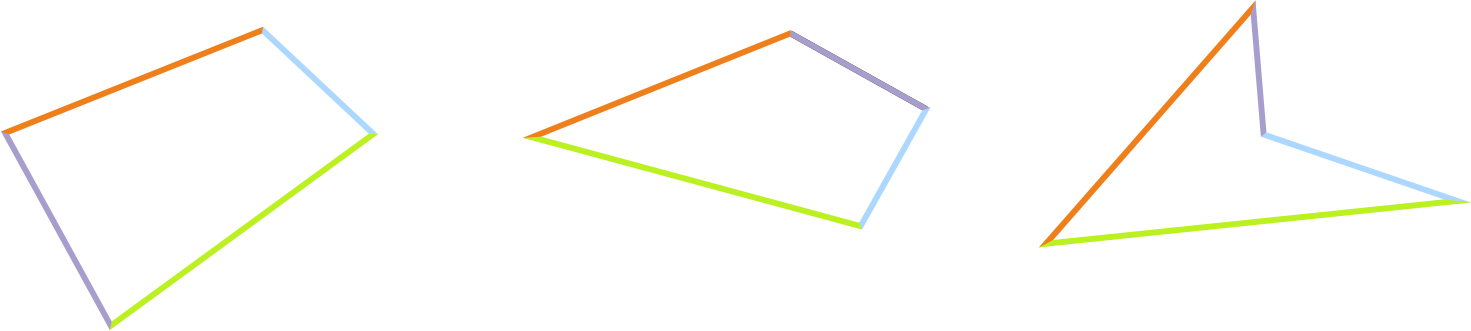
Замкнутая ломаная линия образует геометрические фигуры.
Звенья ломаных при этом не пересекаются.
Многоугольник – это замкнутая ломаная линия.
Многоугольники имеют стороны (звенья ломаной), углы
(образованы двумя отрезками), вершины (точка соединения двух отрезков, вершина
угла).
В зависимости от количества углов каждый многоугольник
имеет свое название – треугольник, четырехугольник, пятиугольник, шестиугольник
и так далее



Обозначают
многоугольники заглавными латинскими буквами по одной на каждую вершину и
читают их последовательно.
Читают так: пятиугольник АВСDЕ, но начать называть многоугольник
можно с любой вершины: ВСDЕА,
СDЕАВ, DЕАВС, ЕАВСD. Назовём стороны, углы и вершины этого
многоугольника.
Стороны
пятиугольника: АВ, ВС, СD,
DЕ, ЕА; углы: ∠A, ∠B, ∠C, ∠D, ∠E; вершины: точки А, В, С, D, Е.
Если сложить длины всех сторон многоугольника, то получится
его периметр (Р).
Вычислить периметр нашего пятиугольника можно по формуле:
Р = АВ + ВС + СD + DЕ +
ЕА
Рассмотрим теперь два представленных семиугольника.
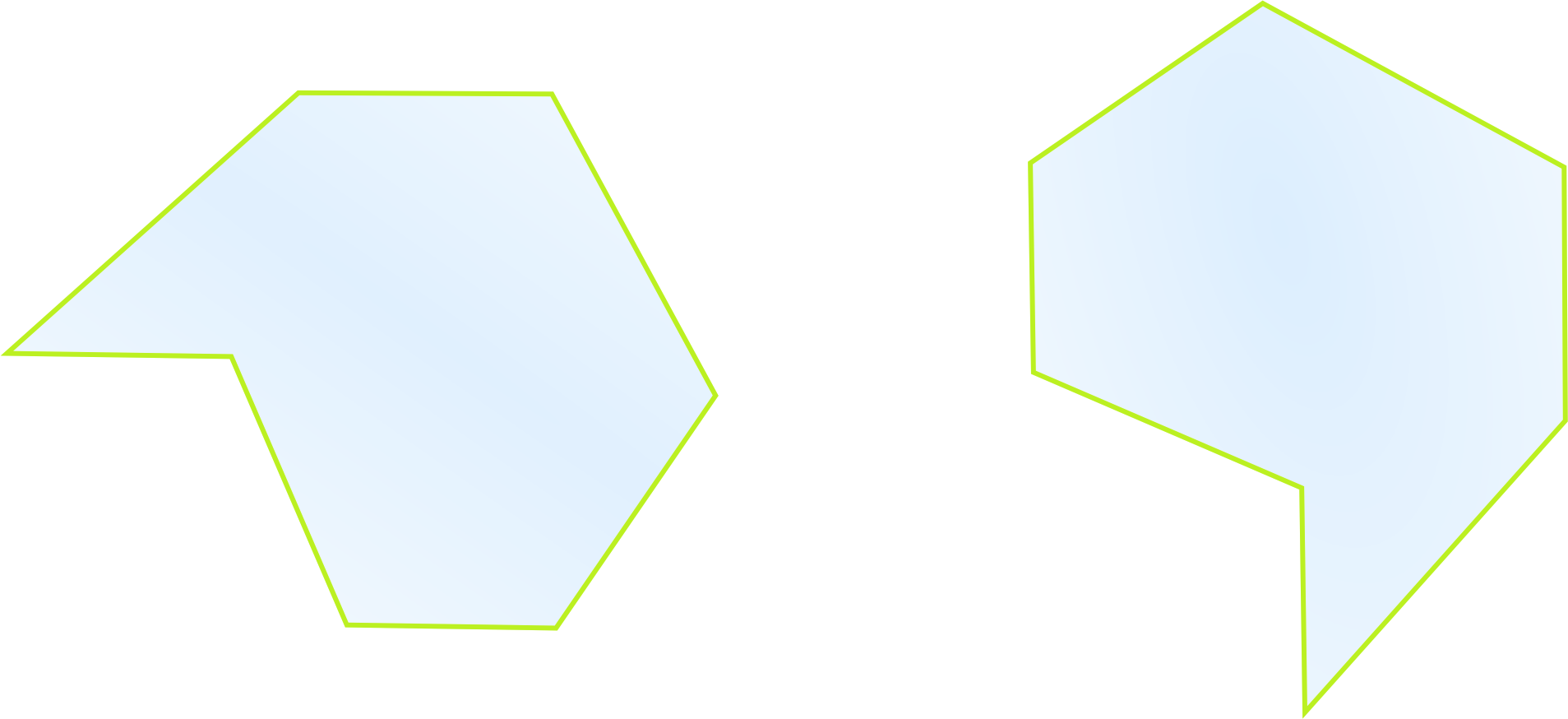
Как
понять, равны ли многоугольники?
Чтобы это выяснить, нужно один многоугольник
наложить на другой.
Если все стороны и вершины у них совпали, то многоугольники
называют равными.
Заключение
В
курсе начальной школы Вы изучали треугольник, квадрат, ромб, прямоугольник,
трапецию и называли их общим словом – многоугольники. Теперь Вы знаете, что
многоугольников существует великое множество. Все они образованы замкнутой
ломаной линией, имеют стороны, углы и вершины. А также каждый имеет свое
название по количеству углов. Теперь Вы знаете, как находится периметр
многоугольника и как понять, равные между собой многоугольники или нет.
0

Аккаунт
Учёба
Статистика
