Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Монотонность функции
Вступление
Вы, наверное, слышали выражение “монотонная речь”. Это непрерывный поток звуков, который не меняется: нет перепадов голоса, смены тембра или каких-либо других резких перепадов. Такая неизменность в целом характеризуем монотонность. Сегодня мы научимся исследовать функции на монотонность. Для этого сначала изучим правила, которые описывают, что происходит с функцией на промежутках, а затем перейдём к алгоритму исследования монотонности функции.
Теория по теме Исследование функции на монотонность
Чтобы исследовать функцию на монотонность, можно нарисовать её график и по нему определить данное свойство.
Например, функция f(x) на интервале монотонно возрастает.
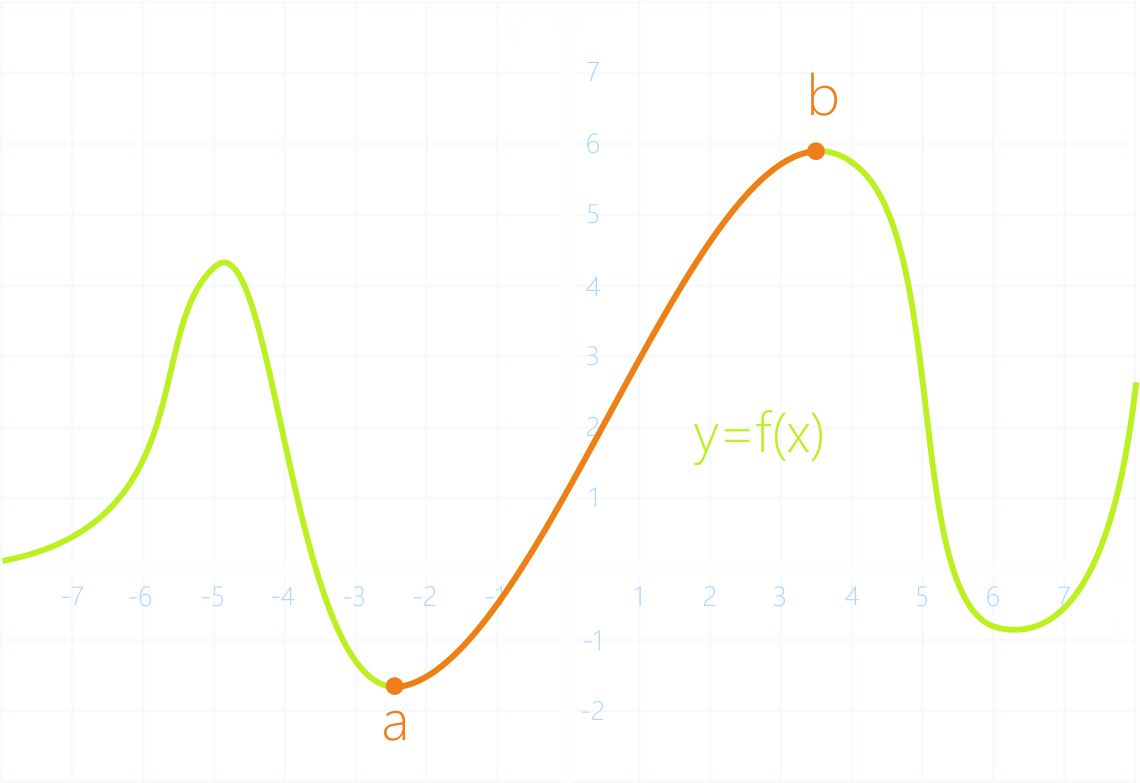
Однако, рисовать график довольно долго и иногда довольно сложно.
Чтобы исследовать функцию на монотонность, быстрее и удобнее использовать понятие производной.
Правило:
Если во всех точках интервала (a;b) существует производная функции y=f(x) и выполняется:
- f?(x)>0, то функция возрастает на промежутке,
- f?(x){|>=|}0, то функция не убывает на промежутке,
- f?(x)<0, то функция убывает на промежутке,
- f?(x){|<=|}0, то функция не возрастает на промежутке.
Исследование функции на монотонность.
Чтобы исследовать функцию y = f(x) на монотонность, необходимо:
- найти f'(x) - производную функции,
- исследовать производную функции и найти интервалы, на которых значение производной одного знака,
- применить правило для каждого интервала.
Заключение
На сегодняшнем занятии нам удалось разобраться в понятии монотонность и проанализировать его в контексте исследования функции. Мы изучили правило, которое описывает, как функция возрастает на промежутке и как функция убывает на промежутке. Кроме того, мы описали пошаговый план исследования функции на монотонность. А теперь потренируемся исследовать функции на монотонность на примере заданий от Виртуального Учителя.
К вашей цели с Виртуальным учителем
