Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
Площадь круга
Вступление
Круг – особенная фигура. Древние греки считали его высшим совершенством, венцом творения. Именно круг - символ бесконечности. Поэтому к нему всегда было пристальное внимание. Мы рассмотрим не весь научный путь, а только результаты труда великих ученых и запомним формулы, которые они вывели для вычисления площади круга. Как найти площадь круга зная диаметр, радиус или длину окружности? Для каждого варианта вводных данных есть своя формула. Давайте разбираться.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Площадь круга
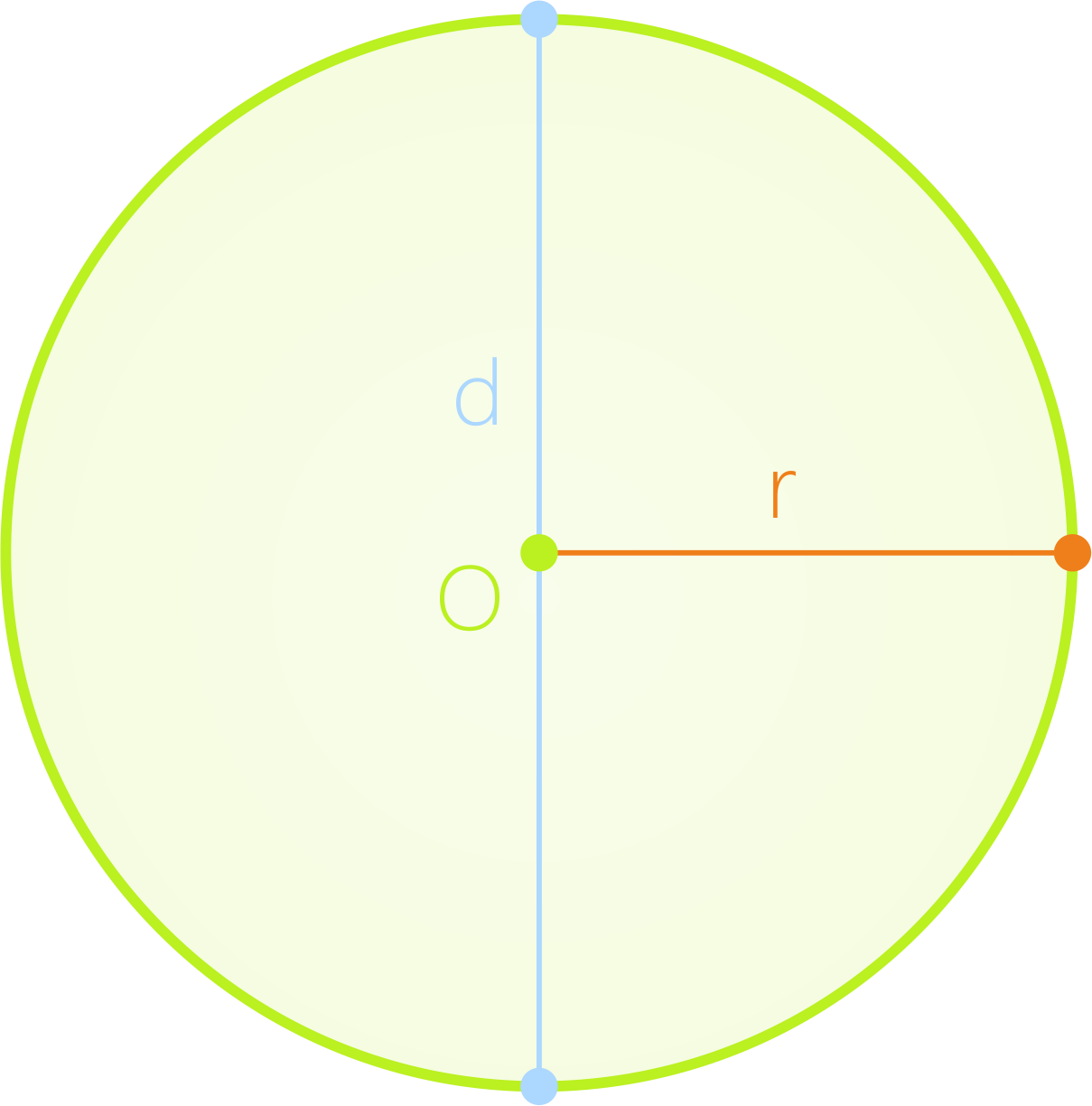
Вспомним, что у круга есть диаметр и радиус, они нам и помогут вычислить его площадь.
Прежде чем писать формулу для вычисления площади круга, нужно ввести дополнительное определение.
Число π (произносится “пи”) - постоянная, равная отношению длины окружности к ее диаметру.
π = 3,1415926535…
Это число имеет бесконечное количество знаков после запятой, поэтому в задачах используют приближенное его значение, равное 3,14 или 3,1415.
Формула для вычисления площади круга, зная его радиус:
S=π*r{|pow|2|}{|!|}{|frac|{|root||}||},
где S - обозначение площади, π - число пи, r - радиус круга.
Вспомним, что диаметр равен удвоенному радиусу, поэтому можем найти площадь круга, зная его диаметр.
Формула для вычисления площади круга, зная его диаметр:
S=π*d{|pow|2|}/4,
где S - обозначение площади, π - число пи, d - диаметр круга.
Вспомним, как связан радиус с длиной окружности: l=2*π*r и найдем площадь круга через длину окружности.
Формула для вычисления площади круга, зная его длину окружности:
S=l{|pow|2|}/(4*π) ,
где S - обозначение площади, π - число пи, l - длина окружности.
Заключение
Сегодня мы изучили площадь круга – тему, изучению которой многие ученые посвятили десятилетия своей жизни! Мы повторили терминологию. Заметили, как важно обращать внимание на формулировку задач, чтобы избежать ошибок. Выучили формулы для нахождения площади круга. Пришло время проверить себя на практических заданиях, которые для вас подготовил Виртуальный Учитель. Нажимайте решать!
К вашей цели с Виртуальным учителем
