Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Площадь сферы
Вступление
Несколько предыдущих занятий было посвящено понятию сфера. У всех геометрических тел, с которыми Вы знакомились ранее, можно было найти площадь поверхности с помощью развёрток. Со сферой так не получится, её невозможно развернуть на плоскость. Для нахождения площади поверхности сферы необходимы другие способы. Давайте рассмотрим, как можно найти площадь сферы. Для этого Вы познакомитесь с понятием описанного около сферы многогранника и увидите, как с его помощью можно найти площадь поверхности сферы.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Площадь сферы
Многогранник называется описанным около сферы, если сфера касается всех его граней. Это значит, что каждая грань такого многогранника является касательной плоскостью к сфере. В таком случае сфера будет называться вписанной в многогранник.
Будем строить последовательность описанных около сферы многогранников так, чтобы размер наибольшей грани каждого следующего многоугольника был меньше, чем у предыдущего.
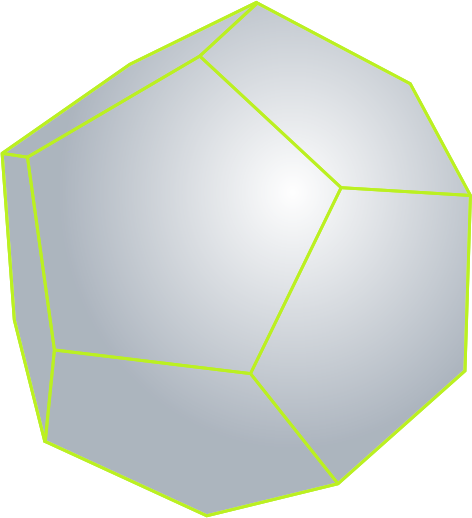
Чем меньше размер граней многоугольника, тем больше количество граней.
Площадь сферы равна пределу такой последовательности описанных многогранников при стремлении размера наибольшей грани к нулю.
Такой предел равен: S{|index|сферы|}= 4πR{|pow|2|}
Таким образом, площадь поверхности сферы равна произведению 4π и квадрата радиуса сферы.
Заключение
Итак, Вы познакомились с понятием описанного около сферы многогранника и вписанной в многогранник сферы и научились находить площадь сферы. Теперь Вы знаете, с помощью какой последовательности действий можно найти площадь поверхности сферы и выучили формулу нахождения площади сферы. Вы уже умеете находить площади поверхностей всех основных пространственных фигур – цилиндра, конуса и сферы.
К вашей цели с Виртуальным учителем
