Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
Решение квадратных уравнений (выбрать один корень)
Вступление
На сегодняшнем занятии мы узнаем, что максимально упрощает поиск корней квадратного уравнения. Конечно же это формула! Как она выглядит, как ее применять, как привести уравнение к нужному нам виду? Что такое дискриминант квадратного уравнения? Все это Вы сегодня узнаете и научитесь применять, ведь мы не только разберем теоретическую часть, но и решим примеры по теме формула корней квадратного уравнения. Итак, приступим!
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Формула корней квадратного уравнения
Чтобы решить квадратное уравнение ax{|pow|2|}+bx+c=0 можно воспользоваться формулой.
Формула корней квадратного уравнения:
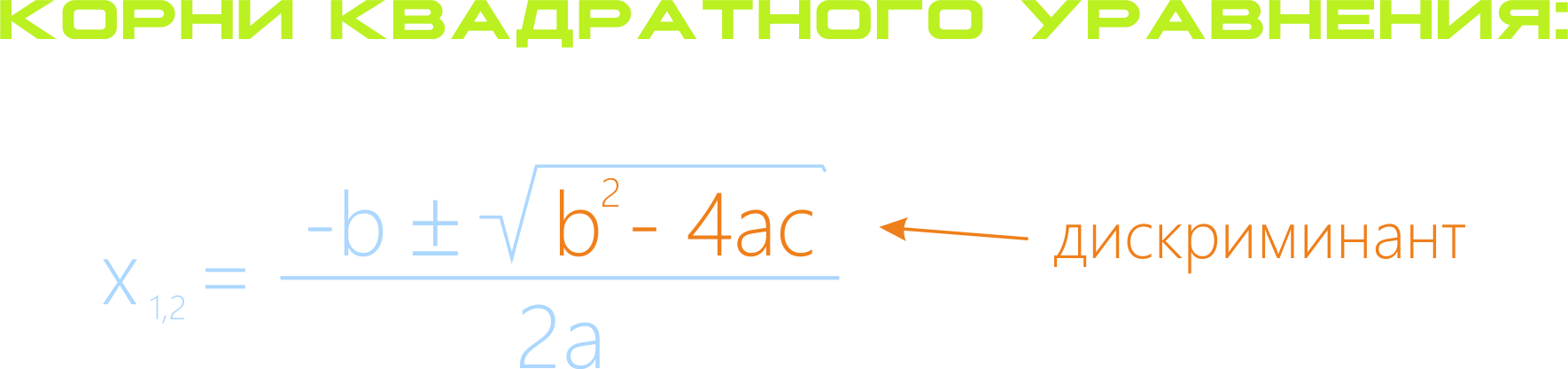
Формулу можно немного переписать, чтобы явно показать значение корней уравнения:
x{|index|1|}={|frac|-b+{|root|b{|pow|2|}-4ac|}|2a|}, x{|index|2|}={|frac|-b-{|root|b{|pow|2|}-4ac|}|2a|}.
Выражение, написанное внутри корня b{|pow|2|}-4ac обозначают буквой D и называют дискриминантом квадратного уравнения.
Правило. Если:
- D<0, то квадратное уравнение не имеет корней,
- D=0, то квадратное уравнение имеет единственный корень,
- D>0, то квадратное уравнение имеет 2 корня.
Так как в формуле корней квадратного уравнения из дискриминанта извлекают корень, а по определению корня, его нельзя извлекать из отрицательного числа, это дает ограничения и на сам дискриминант, поэтому квадратное уравнение может не иметь корней.
Чтобы решить квадратное уравнение, используя формулу, необходимо привести уравнение к стандартному виду: ax{|pow|2|}+bx+c=0.
Заключение
Формула корней квадратного уравнения, которую мы сегодня изучили, пригодится Вам на многих контрольных и проверочных работах. В случае, если данное изначально уравнение имеет вид не стандартный вид, то необходимо провести преобразования и привести данное уравнение к стандартному виду. После чего можно смело применять формулу квадратного уравнения. Давайте потренируемся! Виртуальный Учитель подготовил для Вас новые задания, решая которые Вы легко и быстро научитесь применять формулу квадратного уравнения. Нажимайте кнопку решать и переходите к заданиям.
К вашей цели с Виртуальным учителем

Аккаунт
Учёба
Статистика
