Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Решение простейших неравенств с синусом
Вступление
Перед нами открывается новая тема - простейшие тригонометрические неравенства. Решению тригонометрических неравенств мы посвятим два занятия. Сегодня мы изучим неравенство с синусом. Для того чтобы освоить данную тему, необходимо помнить, что такое единичная окружность и как решать простейшие тригонометрические уравнения - этому мы посвятили последние 4 занятия.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Неравенство sin(a) > b (sin(a) < b)
Чтобы решить простейшие тригонометрические неравенства, необходимо уметь решать простейшие тригонометрические уравнения и знать, что такое единичная окружность.
Вспомним, что число b в уравнении {|sin|α|}=b это ордината точки на единичной окружности, другими словами, это горизонтальная прямая y=b. Таким образом, чтобы решить неравенство вида: {|sin|α|}>b (или {|sin|α|}<b), для начала необходимо отметить на единичной окружности все точки, имеющие ординату, равную b. Для примера будем использовать неравенство вида {|sin|α|}>0,5.
(рисунок единичной окружности с отмеченными точками с ординатой b).
Далее обратим внимание на знак неравенства. Если знак “больше”, тогда необходимо отметить ту дугу окружности, которая выше ординаты b. Если знак неравенства “меньше”, значит, отметим дугу окружности, которая ниже.
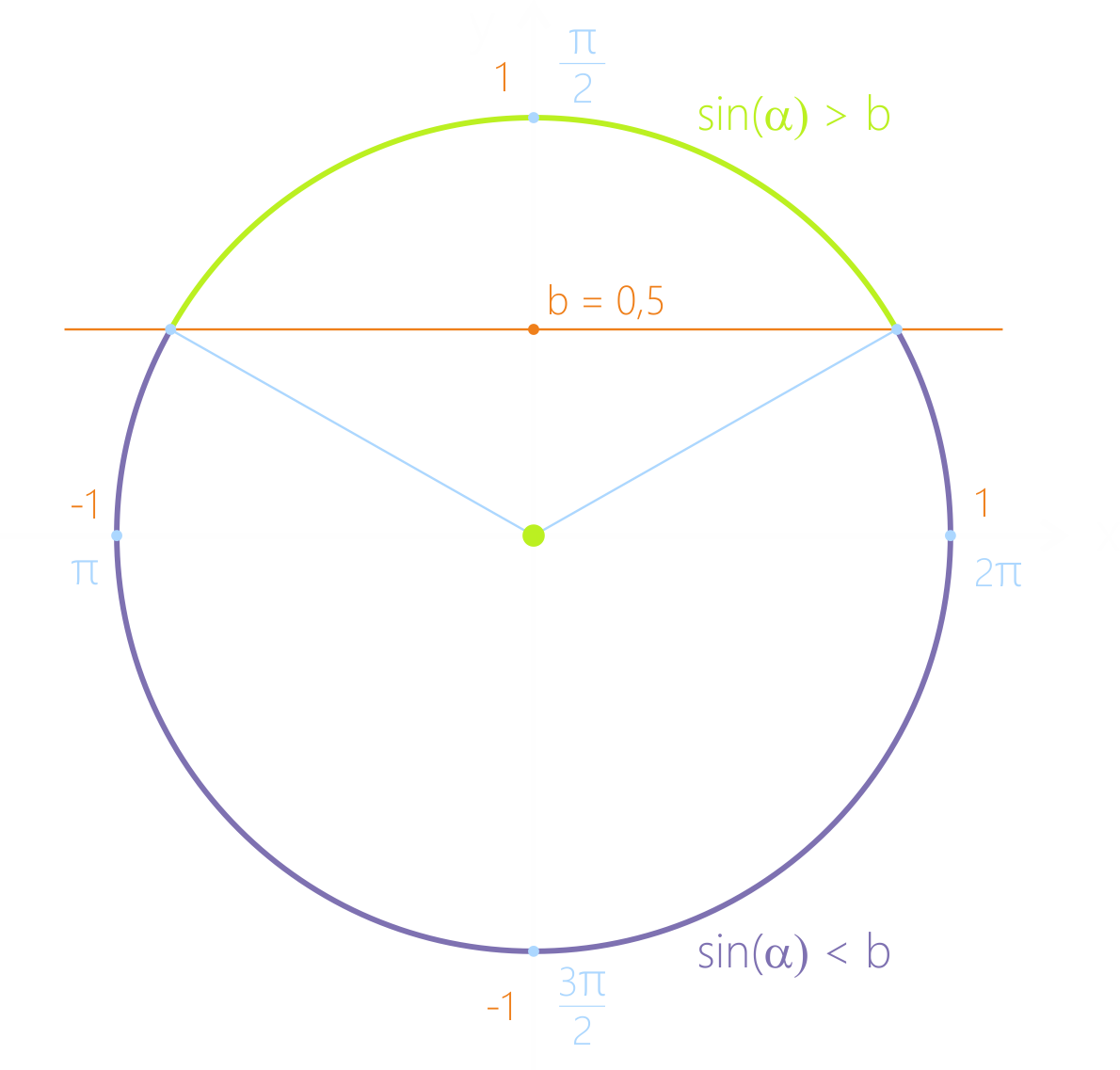
Таким образом, осталось найти значения углов, которым соответствуют граничные точки дуги, это углы:
- {|arcsin|β|}+2{|pi|}k,
- {|pi|}-{|arcsin|β|}+2{|pi|}k.
Далее, решение тригонометрических неравенств сводится к тому, чтобы сказать, что значение самого угла должно быть между найденными граничными значениями точек дуги:
{|arcsin|β|}+2{|pi|}k<a<{|pi|}-{|arcsin|β|}+2{|pi|}k.
Заключение
Как видите, и тригонометрические уравнения не обошлись без единичной окружности. Это связано с тем, что единичная окружность даёт возможность графического изображения всего, что дано нам в задаче, и четкой визуализации того, что мы ищем в задаче. Именно поэтому единичная окружность - ключевой инструмент в решении простейших тригонометрических неравенств. В индивидуальных заданиях, которые подготовил для Вас Виртуальный Учитель у Вас будет возможность применить алгоритм решения, описанный в нашем уроке.
0

Аккаунт
Учёба
Статистика
