Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Решение уравнения tg(x) = a
Вступление
Наш следующий шаг в изучении простейших тригонометрических уравнений - это знакомство с уравнением тангенса. Как решать данный вид уравнений и какие инструменты нам в этом помогут? В чём заключается суть понятия арктангенс и что собрано в таблицу арктангенсов? Обязательно ли учить таблицу тангенсов и таблицу арктангенсов? У нас накопилось много вопросов, давайте вместе найдём ответы на каждый из них.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Уравнение tg(a) = b
Решение уравнения вида {|tg|α|}=b может быть довольно простым, если коэффициент b будет табличным значением.
Например, если:
- {|tg|α|}=1, из таблицы тангенсов можно понять, что α={|frac|{|pi|}|4|} (45 градусов),
- {|tg|α|}={|root|3|}, из таблицы тангенсов можно понять, что α={|frac|{|pi|}|3|} (60 градусов),
- и т.д.
Чтобы найти угол, тангенс которого известен, можно воспользоваться единичной окружностью с осью тангенсов.
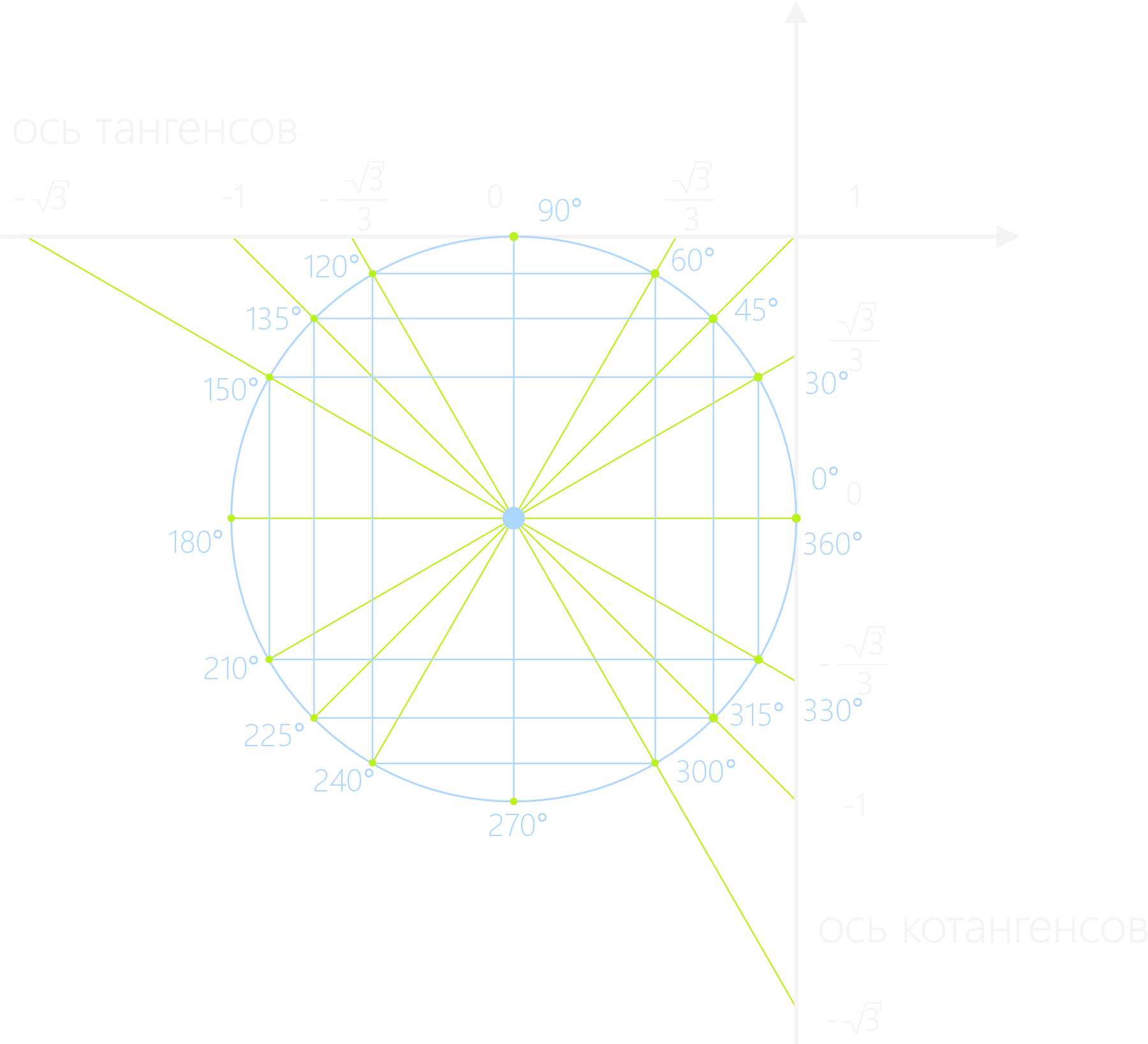
Видно, что углы, имеющие одинаковое значение тангенсов, отличаются на половину окружности, т.е. на радиан.
В случаях, когда значение тангенса угла не табличное, прибегают к использованию арктангенса.
Арктангенс b - это значение угла, тангенс которого равен b. Обозначается: {|arctg|β|}.
Решение уравнений {|tg|α|}=b:
- a={|arctg|β|}+{|pi|}n,
где n - любое целое число.
Приведем таблицу арктангенсов, с помощью которой можно быстро найти угол, если его тангенс является табличным значением.
Таблица арктангенсов
Заключение
Итак, изучен третий вид простейших тригонометрических уравнений - уравнение тангенса. Как Вы заметили, алгоритм решения уравнений остаётся неизменным, равно как и важность знания данных таблиц тангенсов и арктангенсов. И всё же так ли необходимо учить эти значения? Ответ да. Ведь именно знание значений тангенса и арктангенса угла даёт нам возможность существенно сэкономить время при решении задач. Говоря о таких важных экзаменах как ОГЭ и ЕГЭ мы точно знаем, что каждая секунда дорога. Чем меньше времени Вы потратите на простые уравнения, тем больше у Вас останется для более сложных заданий. Поэтому выученные таблицы будут для Вас прекрасной подмогой.
К вашей цели с Виртуальным учителем
