Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Сложение дробей с разными знаменателями
Вступление
Продолжаем изучать обыкновенные дроби. От сложения дробей с одинаковыми знаменателями мы переходим к решению примеров на сложение дробей с разными знаменателями. Это более интересные примеры, требующие знания порядка действий и особенного внимания. Для того чтобы без ошибок решать примеры на сложение обыкновенных дробей, нужно знать некоторые правила. Мы рассмотрим порядок действий при сложении дробей с разными знаменателями, а также разберем алгоритмы двух способов приведения дробей к общему знаменателю. Итак, всё по порядку.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Сложение дробей с разными знаменателями
Чтобы выполнить сложение дробей с разными знаменателями нужно:
- привести дроби к общему знаменателю
- сложить получившиеся числители.
Привести дроби к общему знаменателю можно двумя способами:
- умножить числитель и знаменатель первой дроби на знаменатель второй дроби, а числитель и знаменатель второй дроби умножить на знаменатель первой
- найти НОК знаменателей дробей (наименьшее общее кратное - число, которое делится на оба знаменателя исходных дробей), умножить числитель и знаменатель первой дроби на недостающий множитель знаменателю, чтобы получить НОК, аналогично умножить числитель и знаменатель второй дроби, чтобы получить НОК.
Выполним сложение двух обыкновенных дробей двумя способами:
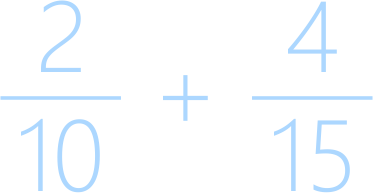
Первый способ:
- приведем дроби к общему знаменателю первым способом:
домножим первую дробь на знаменатель второй, а вторую дробь на знаменатель первой.
- сложим числители дробей, знаменатель оставим тем же:
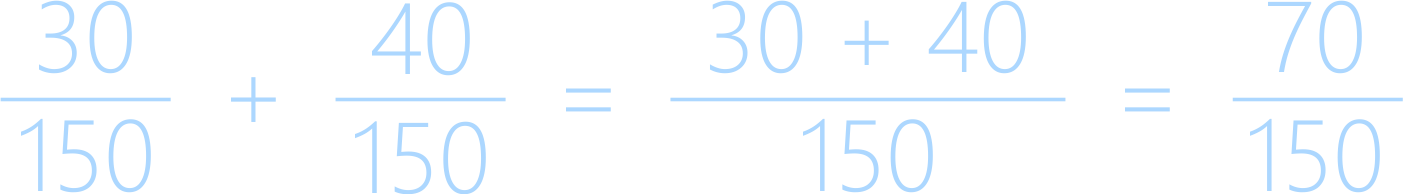
Второй способ:
- приведем дроби к общему знаменателю вторым способом.
Найдем НОК(10, 15) = 30.
Домножим первую дробь на 30:10=3, а вторую дробь на 30:15=2.
- сложим числители дробей, знаменатель оставим тем же:
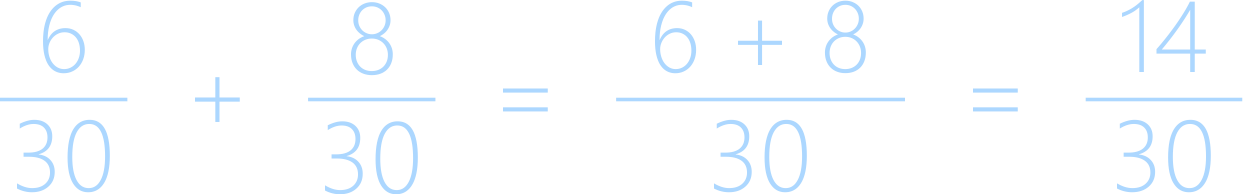
Мы выполнили сложение обыкновенных дробей двумя способами и получили, казалось бы, разные ответы. Вспомним свойство дробей о том, что можно умножать числитель и знаменатель дроби на одно и то же число, от этого дробь не изменится, аналогично выполняется свойство и с делением.
Свойство дроби: если разделить числитель и знаменатель дроби на одно и то же число, то сама дробь не изменится. Данное действие называется сокращением дроби.
Воспользуемся этим свойством и сократим первую дробь на 10, а вторую дробь на 2:
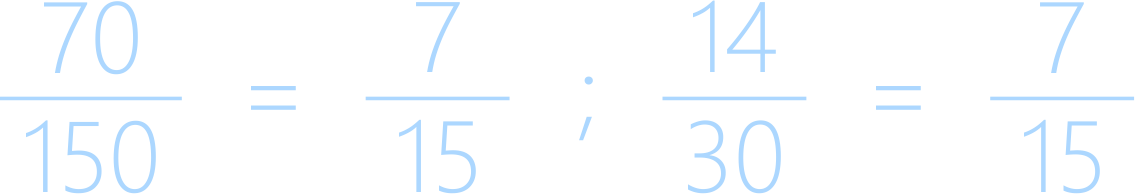
Видно, что результат получился одинаковым, а значит оба способа приведения дробей к общему знаменателю верные.
Первый способ рекомендуется при сложении обыкновенных дробей, имеющими небольшие знаменатели, второй способ рекомендуется при действиях с дробями, имеющими большие знаменатели.
Заключение
Сегодня мы с Вами освоили ещё одну тему! Это сложение дробей с разными знаменателями. Мы узнали, что нужно сделать, чтобы привести дроби к общему знаменателю. Рассмотрели оба возможных способа и сравнили результат. Запомнили последовательность действий и изучили форму записи решения. Мы познакомились с новым термином НОК наименьшее общее кратное. Запомните его, он еще много раз пригодится Вам при произведении арифметических действий с дробями, у которых разные знаменатели. Пришло время выполнить задания! Виртуальный Учитель подготовил для Вас новые примеры на сложение дробей с разными знаменателями. Нажимайте решать.
К вашей цели с Виртуальным учителем
