Сокращение дробей

Обыкновенные дроби содержат в числителе и знаменателе натуральные числа. Они могут быть многозначными. Выполнять действий с многозначными числами сложнее, чем с однозначными или хотя бы двузначными. С помощью знания основного свойства дроби мы можем сделать числа в числителе и знаменателе меньше. Тогда и вычисления будут проще. Для этого нужно сократить дробь.

Сократить, значит разделить числитель и знаменатель на любое одинаковое число, кроме нуля и единицы. Делить на нуль нельзя, на единицу – бессмысленно, ведь при делении на единицу числа не изменятся.

После сокращения мы получим новую дробь, где числитель и знаменатель выражены новыми числами. Но исходная и сокращенная дроби будут равны.

Когда сокращают дроби, действуют по алгоритму:

1. Находят общий множитель числителя и знаменателя.

2. Делят на него числитель и знаменатель.

3. Оформляют графически: числитель и знаменатель зачеркивают простым карандашом диагональной чертой, карандашом подписывают, какой результат получился при делении. Затем записывают результат.

4. Записывают новую дробь.

Общим множителем будет 2. Разделим и числитель, и знаменатель на 2. Если сократим дробь на 2, получим:

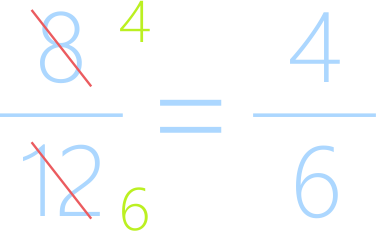
Но данный результат не будет окончательным, потому что числа 4 и 6 можно ещё раз разделить на 2.

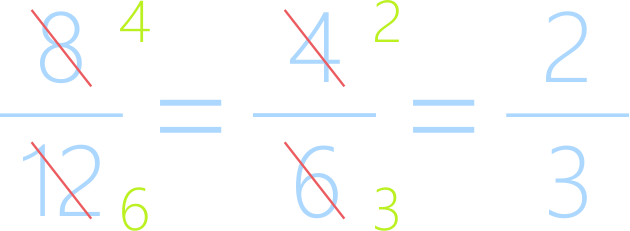
Дробь, у которой числитель и знаменатель уже нельзя разделить ни на одно число, кроме 1, называется несократимой.

Мы видим, что для сокращения дроби нам пришлось сделать два действия. Но можно сделать это быстрее, в одно действие. Общий множитель числителя и знаменателя равен 4.

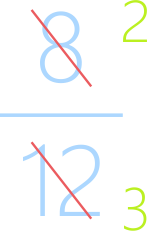
Записываем итог:

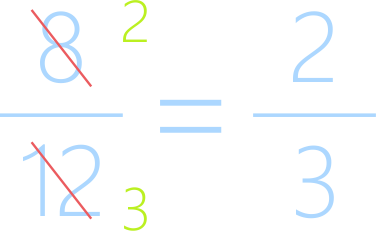
Цель сокращения – достижение несократимой дроби.

Для простоты вычислений используют основное свойство дроби и прём сокращения дробей. Чтобы не оперировать большими числами, дроби сокращают. Несократимые дроби легче и быстрее складывать и вычитать. Сокращения дробей пригодятся Вам при нахождении значений выражений с дробями. Вычисления с сокращёнными дробями проводить удобнее.