Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Сравнение дробей
Вступление
Итак, мы познакомились с обыкновенными дробями и их разновидностями правильными и неправильными дробями. Мы знаем их характеристики и особенности. Сегодня мы научимся сравнивать обыкновенный дроби между собой. Такое задание регулярно встречается на проверочных и самостоятельных работах. Оно часто пугает учеников или вызывает волнение. При этом если понять, что необходимо знать для сравнения обыкновенных дробей, то такие задания на сравнение перестанут пугать и вызывать волнение. Так что же нужно знать? Давайте разбираться!
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Сравнение обыкновенных дробей
Как мы уже знаем, дроби нужны, чтобы говорить о какой-то части от целого.
Давайте поговорим о том, как сравнивать дроби.
Допустим, нам нужно сравнить четыре седьмых и две трети.
Согласитесь, очень неудобно сравнивать части, когда знаменатели дробей разные, т.е. когда целое в одном случае поделено на семь равных частей, а в другом случае на три равные части.
Чтобы сравнить данные дроби, нужно разделить целое на одинаковое количество частей в первом и во втором случае.
Так как целое делилось в первом случае на 7 частей, а во втором случае на 3 части, то сейчас нам нужно разделить целое на такое число частей, которое делится и на 7 и на 3.
Найдем число, которое делится на 7 и на 3, это число 21.
Значит, если у первой дроби было общее количество частей 7, а станет 21, т.е. в 3 раза больше, то и количество кусочков, которые взяли, станет в 3 раза больше: 4*3=12.
Аналогично действуем со второй дробью: количество всех кусочков увеличивается с 3 до 21, т.е. становится в 7 раз больше, значит, и количество кусочков, которые взяли, тоже станет в 7 раз больше 2*7=14.
В данном случае мы числитель и знаменатель первой дроби умножили на 3, а числитель и знаменатель второй дроби умножили на 7.
Получили:
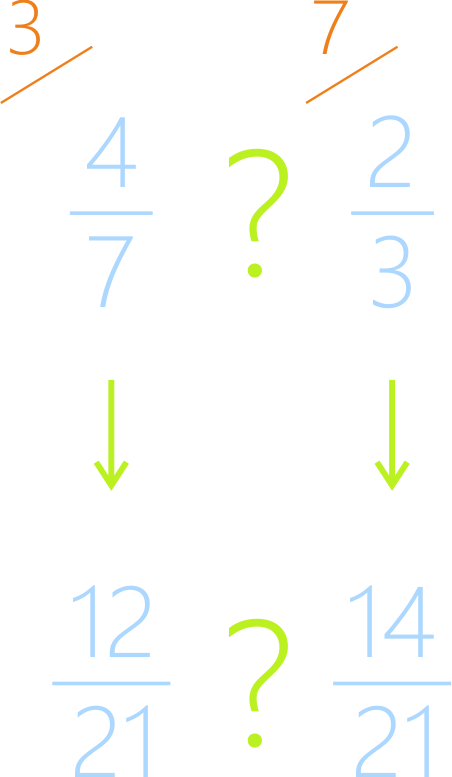
Свойство дроби: если числитель и знаменатель дроби умножить на одно и то же число, то значение дроби не изменится.
После того как обыкновенные дроби приведены к общему знаменателю, их стало довольно легко сравнить.
Правило сравнения дробей с одинаковым знаменателем: если знаменатель первой дроби больше знаменателя второй дроби, то и сама первая дробь больше второй.
В данном примере знаменатель второй дроби равен 14, а знаменатель первой дроби равен 12, значит вторая дробь больше:
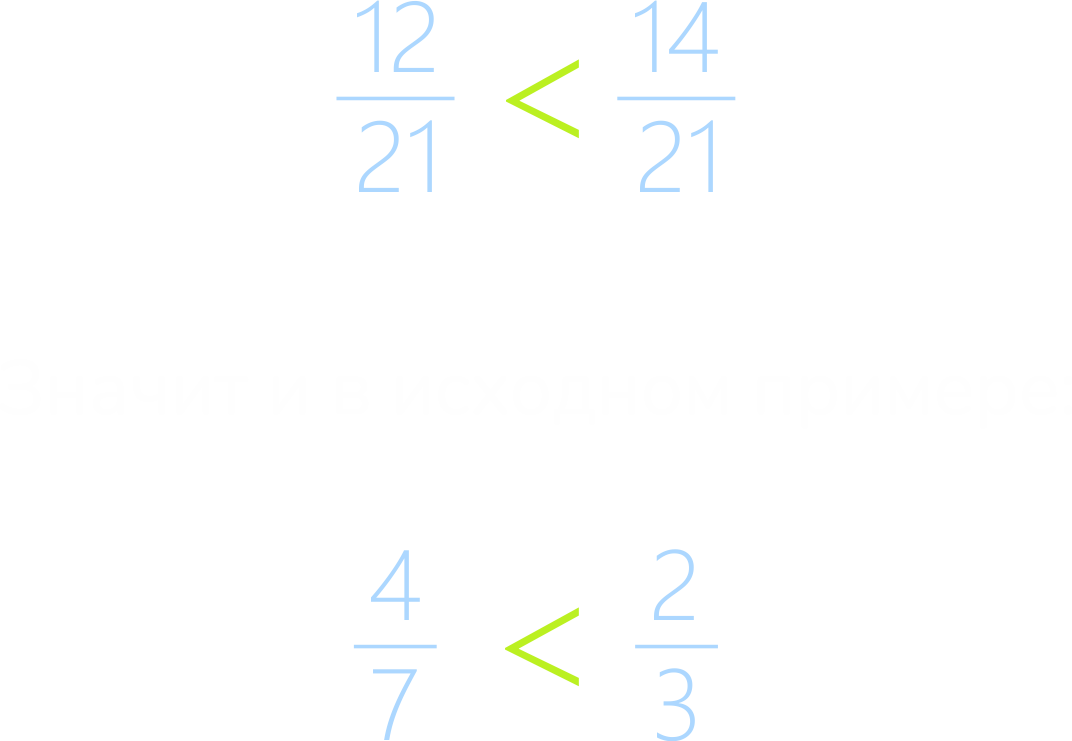
Мы разобрали случай со сравнением обыкновенных правильных дробей, в случае сравнения неправильных дробей производятся аналогичные действия.
Заключение
Итогом сегодняшнего занятия мы можем смело назвать умение проводить сравнение обыкновенных дробей. Мы с Вами вспомнили, что такое обыкновенные дроби, и каких видов они бывают. Как записываются дроби и как называются их части. Узнали, что для того, чтобы сравнить две дроби, нужно привести их к общему знаменателю. Выяснили, как находить общий знаменатель для правильной и неправильной дроби.
Узнали, что когда знаменатели равны, остается сравнить только числители, при этом важно запомнить, что в завершении решения мы ставим знак сравнения именно в исходном примере, а не в том, который получился после наших преобразований.
Давайте закрепим на практике то, что мы сегодня изучили. Нажимайте кнопку решать и переходите к заданиям от Виртуального Учителя.
К вашей цели с Виртуальным учителем
