Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Угол между скрещивающимися прямыми
Вступление
Мы продолжаем рассматривать углы в пространстве. Угол между прямыми - достаточно распространённое понятие в стереометрии. Сегодня Вы научитесь находить углы между любыми прямыми в пространстве. Из курса планиметрии Вы знаете, как искать угол между пересекающимися прямыми. Вы вспомните, как именно его можно найти. Затем этот алгоритм поможет Вам найти угол между скрещивающимися прямыми. Таким образом Вы всегда сможете находить угол между двумя прямыми.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Угол между прямыми
Угол между пересекающимися прямыми:
В пересечении пересекающихся прямых образуется четыре угла. Углом между прямыми является меньший из них (на рисунке угол γ). Таким образом угол между пересекающимися прямыми острый или прямой.
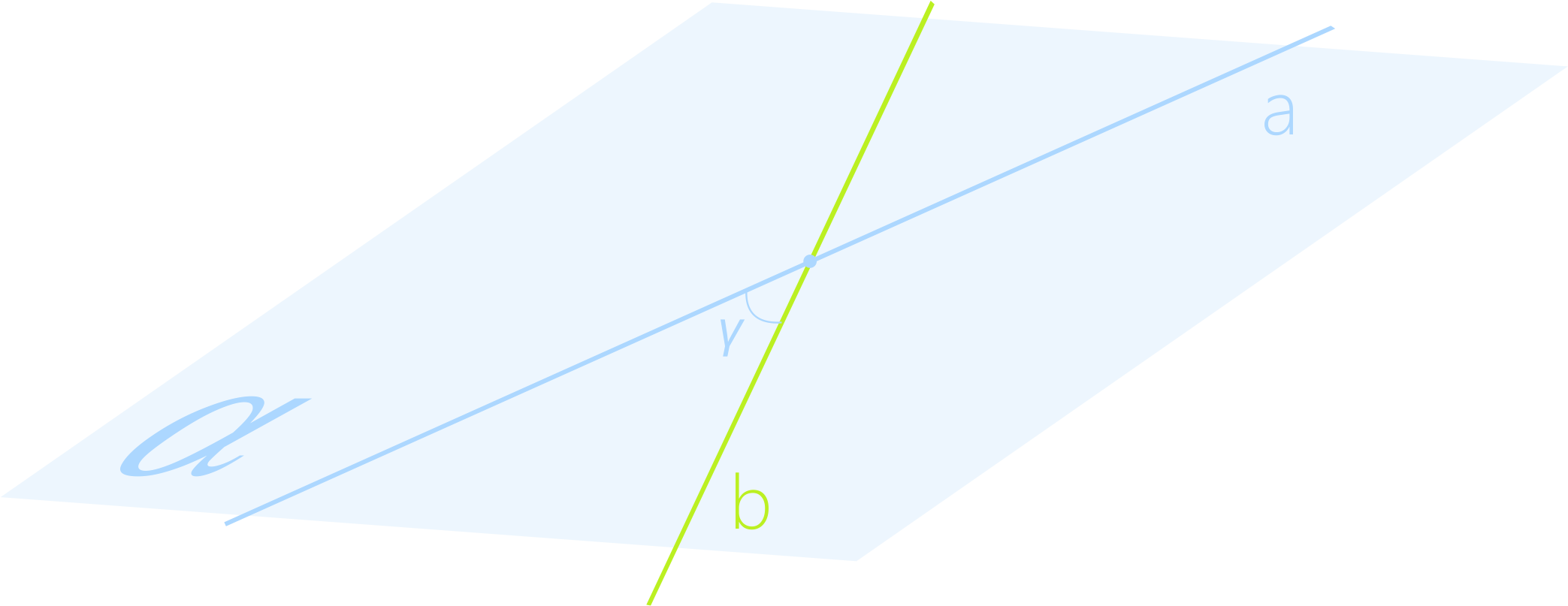
Угол между скрещивающимися прямыми:
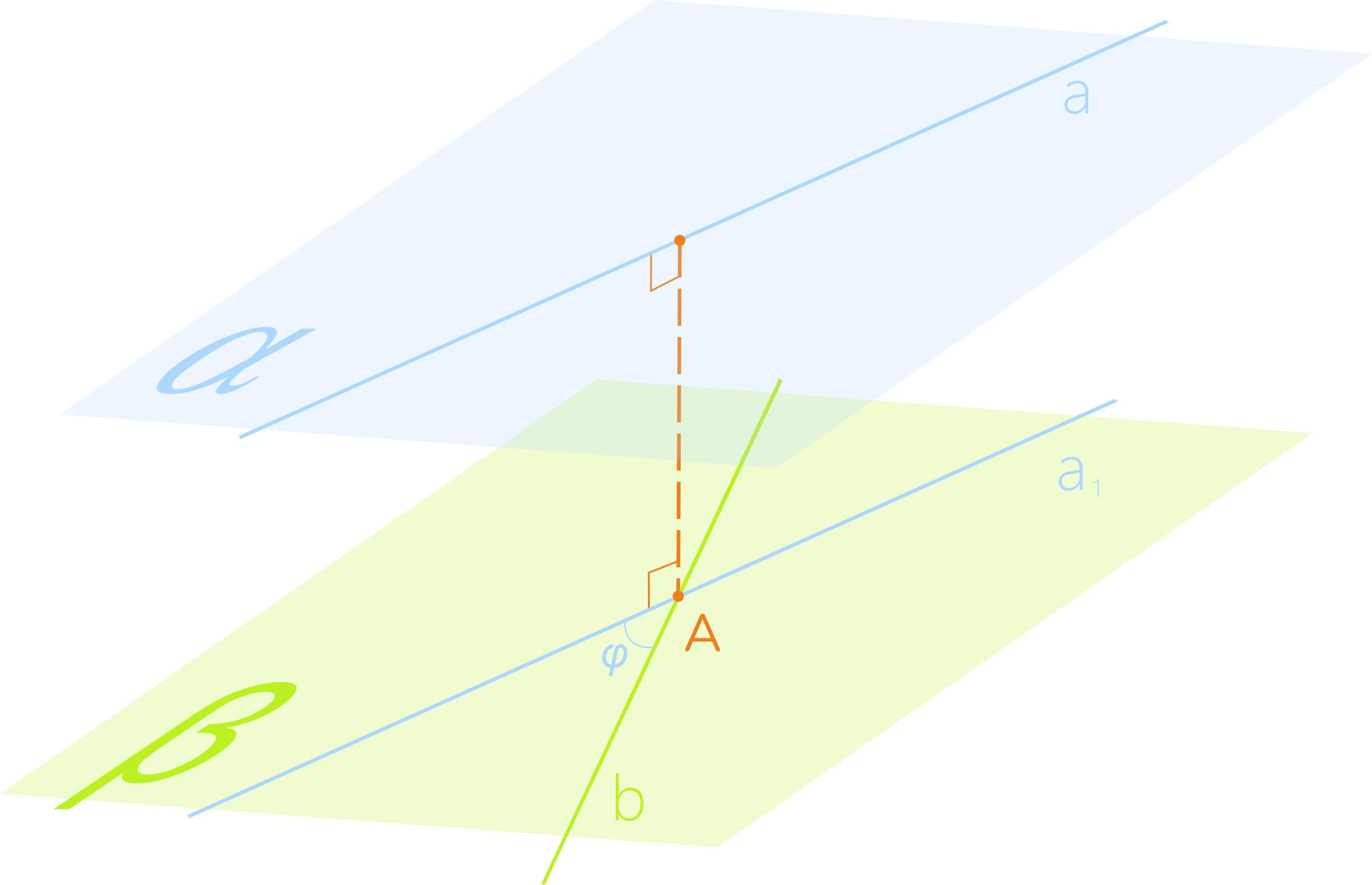
Мы с Вами видим, что прямые a и b не пересекаются. Они находятся в разных плоскостях. При этом, они не параллельны. Такие прямые называются скрещивающимися прямыми.
Для нахождения угла между ними, возьмём произвольную точку A на одной из прямых, например на прямой b. Проведём через неё прямую, параллельную прямой a. Угол между этими прямыми и есть угол между скрещивающимися прямыми. Заметим, что угол между прямыми не зависит от выбора точки A.
Заключение
Сегодня Вы разобрались, как найти угол между данными прямыми в пространстве. Сначала Вы вспомнили, как найти угол между двумя пересекающимися. Затем мы начали рассматривать скрещивающиеся прямые. При помощи параллельного переноса нам удалось найти угол и между скрещивающимися прямыми. Таким образом Вы всегда можете найти угол между прямыми в пространстве.
К вашей цели с Виртуальным учителем
