Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Превообразная
Вступление
Сегодня Вы познакомитесь с важным алгебраическим понятием. Вы узнаете, что такое первообразная. Понятие первообразной связано с понятием производной. Как именно, Вы поймёте на сегодняшнем занятии. Вы вспомните, как считать производные, затем Вы сможете посчитать первообразную. А что будет, если первообразных двух функций будут отличаться на константу? Это наблюдение поможет нам в изучении дальнейших тем.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Первообразная
F(x) - первообразная функции f(x) на промежутке X, если f(x) - производная функции F(x), то есть F?(x)=f(x).
Заметим, что если F{|index|1|}(x)=F{|index|2|}(x)+C, где C - это какая-либо константа, то их производные равны.
Соответственно мы сможем вычислить первообразную с точностью до константы.
То есть константу первообразной мы никогда не узнаем, однако оставшуюся часть, которая зависит от аргумента, мы всегда сможем посчитать.
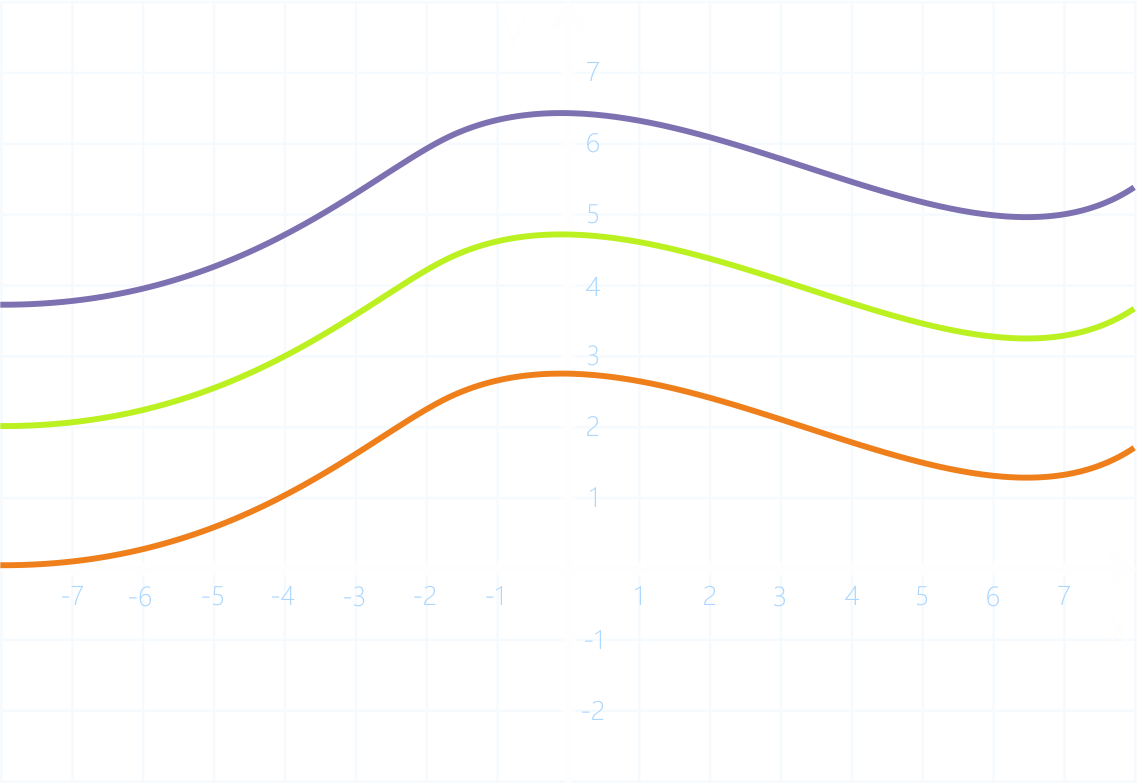
Графики первообразных, которые отличаются только константой
Например, если функция 2x+3, то её первообразная равна x{|pow|2|}+3x+C, где С - это константа.
Например, функции x{|pow|2|}+3x+5, x{|pow|2|}+3x+1, x{|pow|2|}+3x-10 - это первообразные функции 2x+3.
Заключение
Сегодня Вы познакомились с новым понятием в алгебре. Для многих функций существуют обратные им. Например, сложение и вычитание, умножение и деление, возведение в степень и взятие логарифма. Для производной обратной функцией является взятие первообразной. Вы узнали, что невозможно точно посчитать константу в первообразной, поэтому получившиеся функции записываются, как F(x)+C.
К вашей цели с Виртуальным учителем
