Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Разложение на простые множители
Вступление
Тему
«Разложение на простые множители» изучают, чтобы научиться быстро выполнять
операции с дробями. Сами по себе действия с дробями требуют концентрации
внимания и сосредоточенности. Научившись быстро оперировать числами,
раскладывать сложные на простые множители, при работе с дробями Вы будете быстро
и правильно выполнять вычисления.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Разложение на простые множители
Для изучения новой темы надо вспомнить, что такое простое
число.
Для этого выполним задание: найди все множители чисел 3, 8,
10, 11.
Мы видим, что числа 3 и 11 делятся на 1 и на само себя
без остатка. Других делителей у них нет, это простые числа.
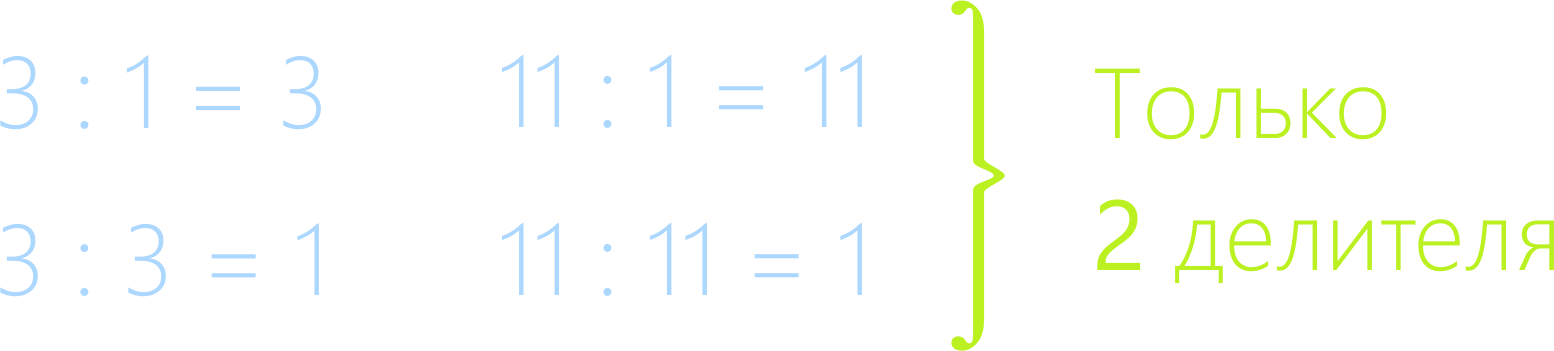
Простые числа
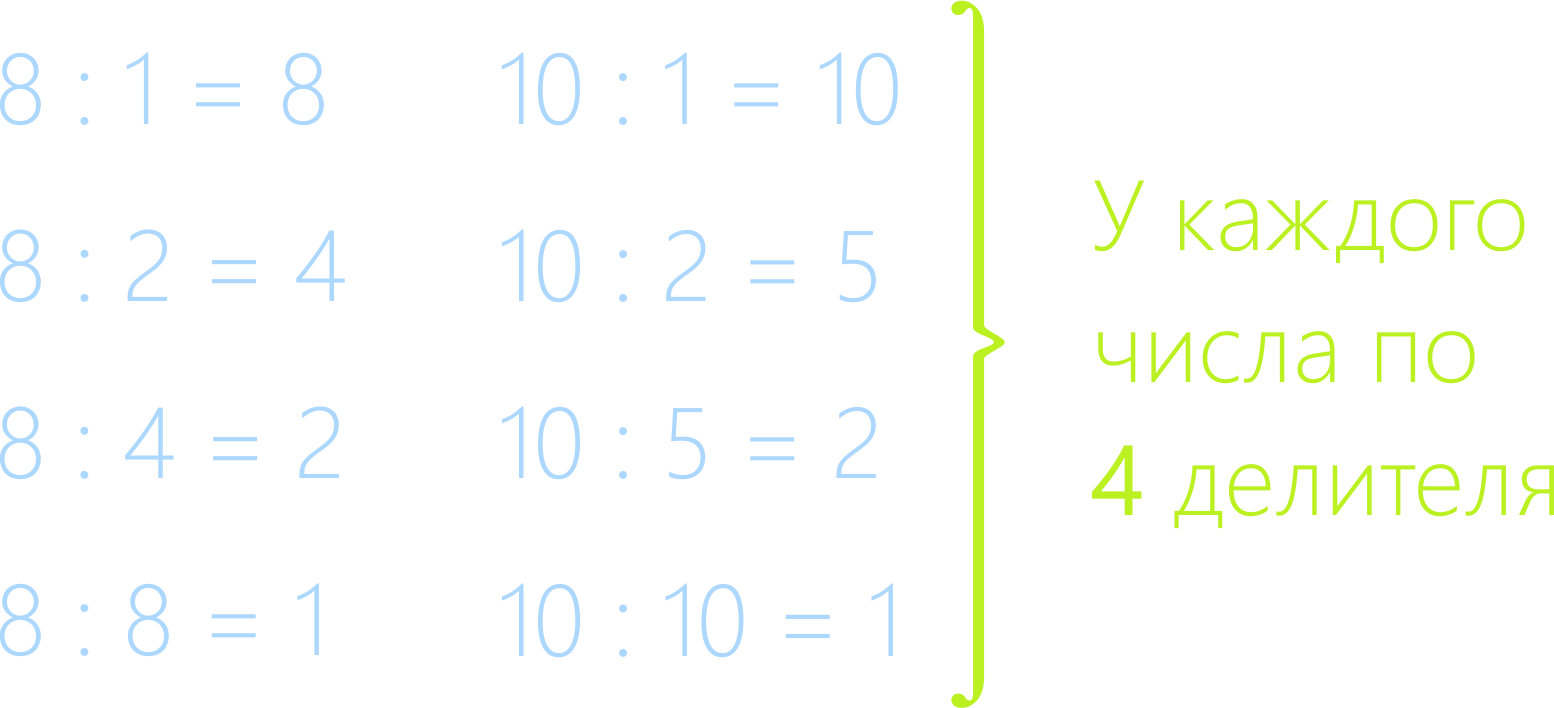
Сложные числа
Числа
8 и 10 имеют и другие делители, не только 1 и само исходное число. Это сложные
числа. Их можно разложить на простые множители.
Как это сделать?
Находим самое маленькое простое число, кроме единицы, на
которое разделится заданное. Делим и записываем промежуточный результат. Дальше
полученное при делении число снова делим на наименьшее простое. И так, пока не
закончится деление.
Рассмотрите процесс деления.
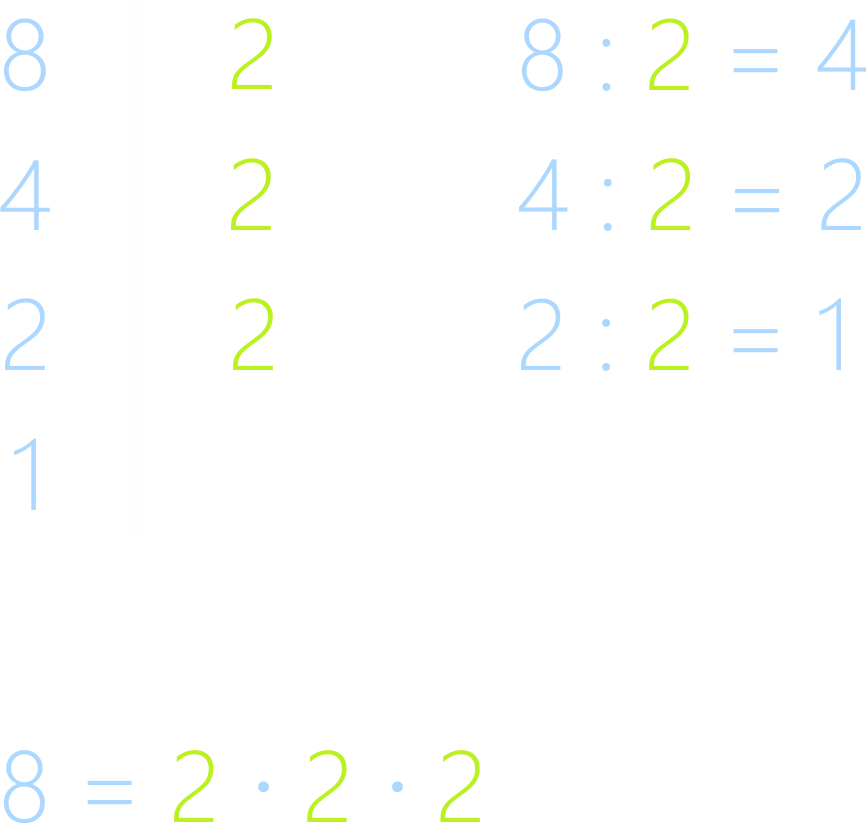
Аналогично разложим на множители число 10.
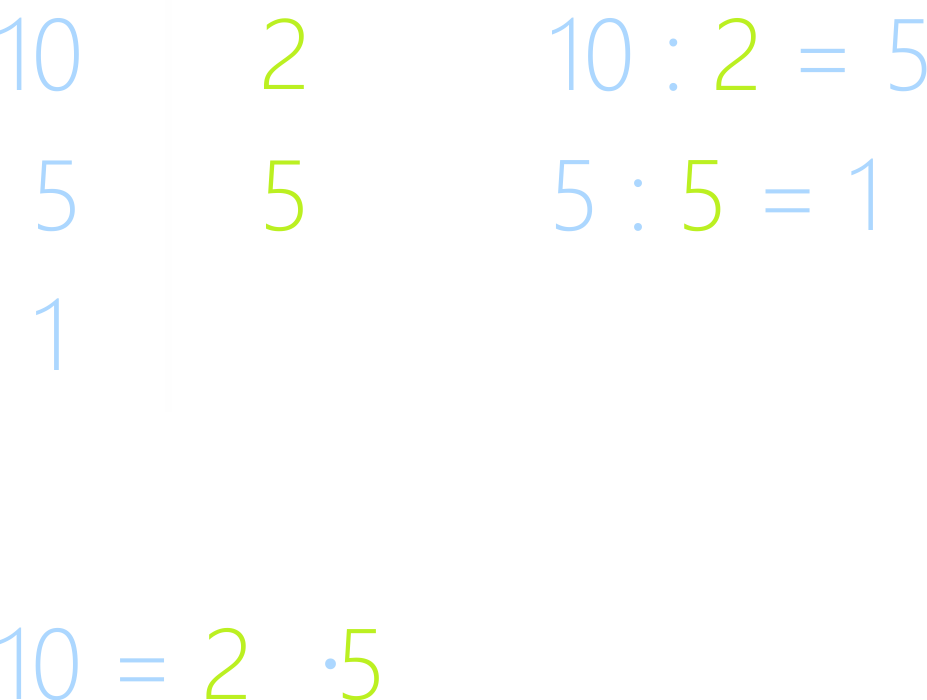
Рассмотрим
процесс разложения с большими числами.
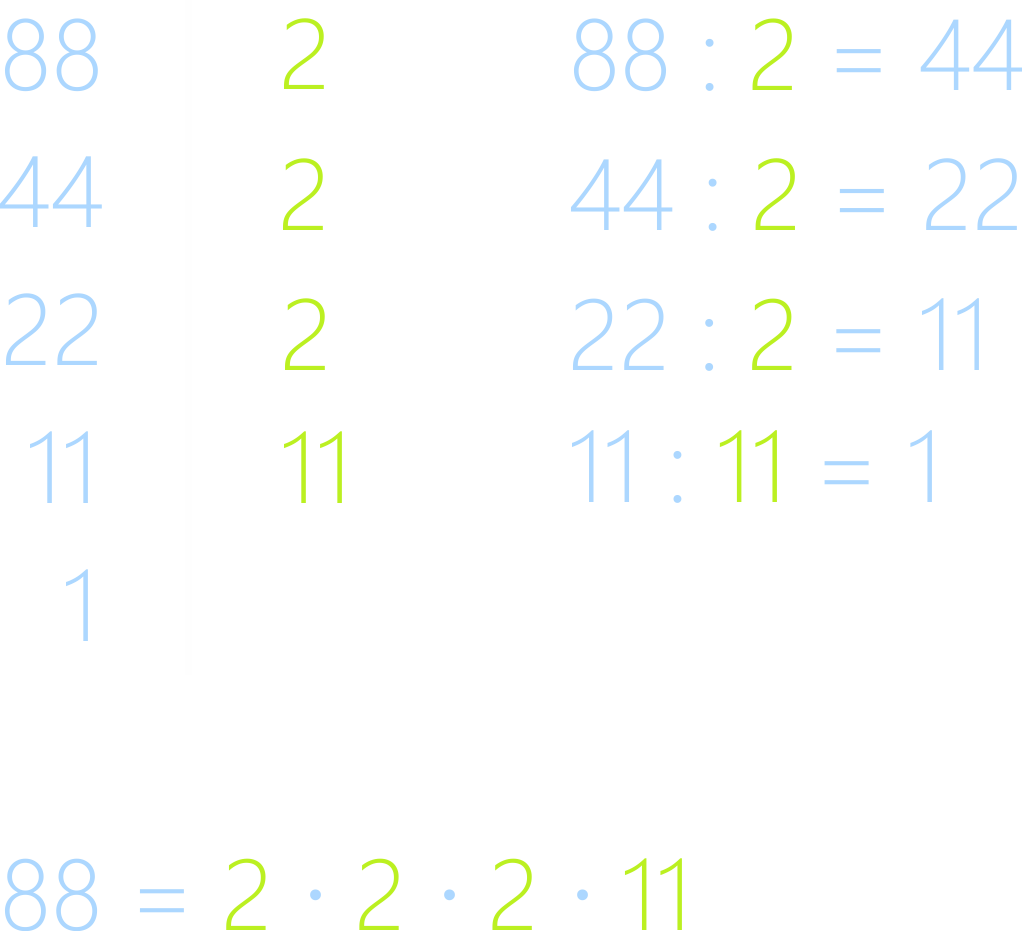
Обратим внимание на то, что количество множителей не зависит от величины числа.
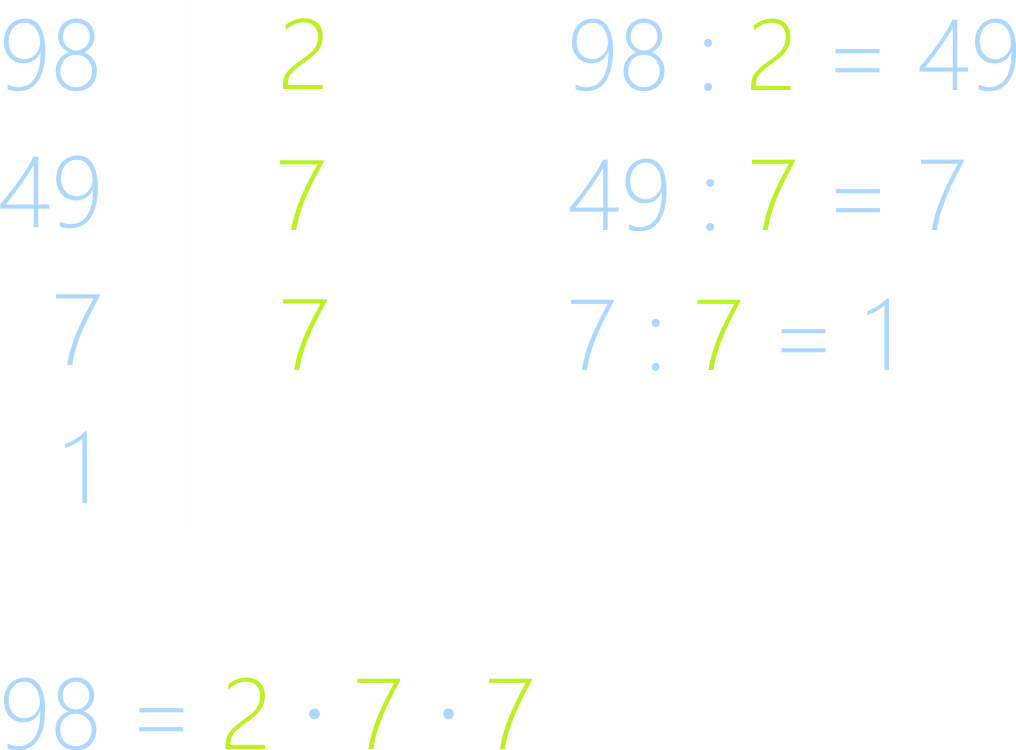
При записи в тетради вычисляют устно, а записывают только
столбик с множителями.
Заключение
Процесс
разложения на простые множители связан с понятием простого числа. Для быстрого
разложения числа н простые множители нужно отлично знать табличное умножение,
знать признаки делимости на некоторые числа: 2, 3, 5. Это поможет быстро
раскладывать числа на простые множители, а в будущем быстро производить
вычисления с дробями.
0

Аккаунт
Учёба
Статистика
