Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Сфера и шар. Уравнение сферы.
Вступление
Вы уже знаете такие пространственные фигуры, как цилиндр и конус. Пришло время рассмотреть ещё одно геометрическое тело, которое называется сфера. Вы узнаете, что это за фигура, и как она образуется. Вы познакомитесь с тем, где находится центр сферы, узнаете, чему равен радиус сферы и как найти её диаметр. Вы увидите, что представляет собой уравнение сферы в прямоугольной системе координат. С понятием сферы связано такое геометрическое тело как шар. Вы узнаете, в чём различие этих фигур и каким неравенством задаются все точки, принадлежащие шару.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Сфера и шар. Уравнение сферы.
Рассмотрим произвольную точку пространства O.
Сфера – это поверхность, образованная всеми точками пространства, расположенными на заданном расстоянии от точки O.
Точка O – это центр сферы.
Радиус сферы R – это расстояние, на котором расположены все точки сферы от центра.
Диаметр сферы – это отрезок, соединяющий две произвольные точки сферы и проходящий через её центр. Он равен удвоенному радиусу: D = 2R.
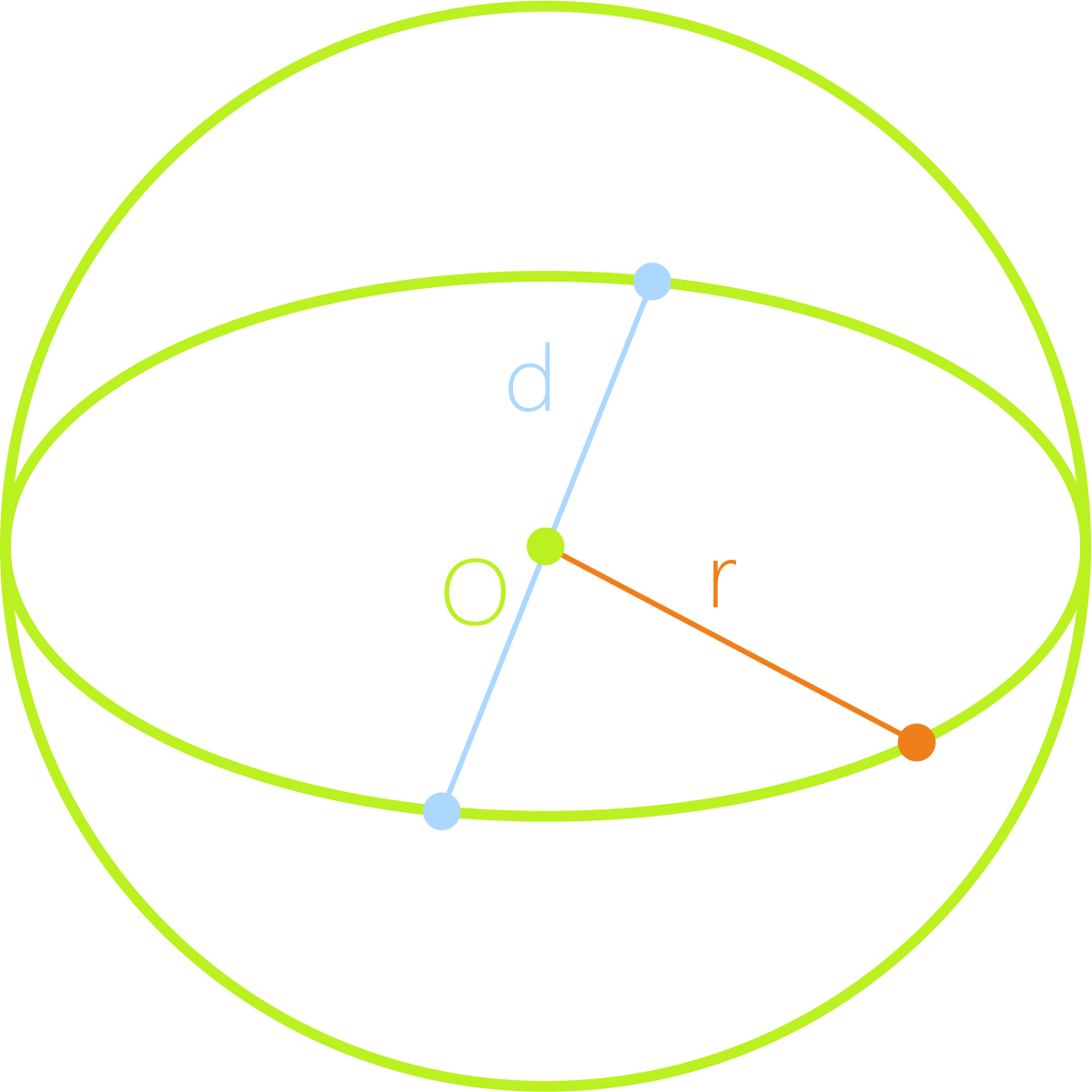
Сфера
Шар – это тело, ограниченное сферой.
Центр, радиус и диаметр шара совпадают с центром, радиусом и диаметром ограничивающей его сферы. Любая точка шара M должна удовлетворять следующему неравенству:
OM ≤ R
Шар
Рассмотрим в прямоугольной системе координат сферу с центром O(x{|index|0|}, y{|index|0|}, z{|index|0|}) и радиусом R. Рассмотрим её произвольную точку M. Расстояние от точки M до центра сферы равно: {|abs|OM|} = {|root|(x - x{|index|0|}){|pow|2|} + (y - y{|index|0|}){|pow|2|} + (z - z{|index|0|}){|pow|2|}|}
Так как точка M лежит на сфере, то {|abs|OM|} = R и OM{|pow|2|} = R{|pow|2|}. Тогда уравнение сферы имеет вид:
(x - x{|index|0|}){|pow|2|} + (y - y{|index|0|}){|pow|2|} + (z - z{|index|0|}){|pow|2|} = R{|pow|2|}
Все точки, удовлетворяющие данному уравнению, лежат на сфере с центром O(x{|index|0|}, y{|index|0|}, z{|index|0|}) и радиусом R.
Все точки, лежащие в шаре с центром O(x{|index|0|}, y{|index|0|}, z{|index|0|}) и радиусом R должны удовлетворять следующему неравенству:
(x - x{|index|0|}){|pow|2|} + (y - y{|index|0|}){|pow|2|} + (z - z{|index|0|}){|pow|2|} {|<=|} R{|pow|2|}
Заключение
На сегодняшнем занятии Вы познакомились с такими новыми понятиями, как сфера и шар. Теперь Вы знаете, что такое центр сферы, умеете находить радиус сферы и диаметр сферы. Вы узнали, чем шар отличается от сферы и с помощью какого неравенства задаются все точки шара в прямоугольной системе координат. Вы познакомились с уравнением сферы и знаете, как по нему определить принадлежность точки данной сфере. Осталось закрепить новые знания на практике. Приступайте к выполнению заданий от Виртуального Учителя.
К вашей цели с Виртуальным учителем
