Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Основное тригонометрическое тождество
Вступление
Для решения множества тригонометрических задач
применяют основное тригонометрическое тождество. На его основе легко вычислить
синус, косинус угла, зная лишь одно из значений. Чтобы понять и доказать
тождество нужно вспомнить, что все эти тригонометрические функции
взаимосвязаны. Основное тригонометрическое тождество действует для любых углов.
Сейчас Вы с ним познакомитесь, а также потренируетесь применять его в решении
задач.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Основное тригонометрическое тождество
Основное тригонометрическое тождество:
sin{|pow|2|}α+cos{|pow|2|}α=1
Рассмотрим
доказательство тождества. Для этого построим единичную окружность с центром О.
Теперь построим произвольный угол α.
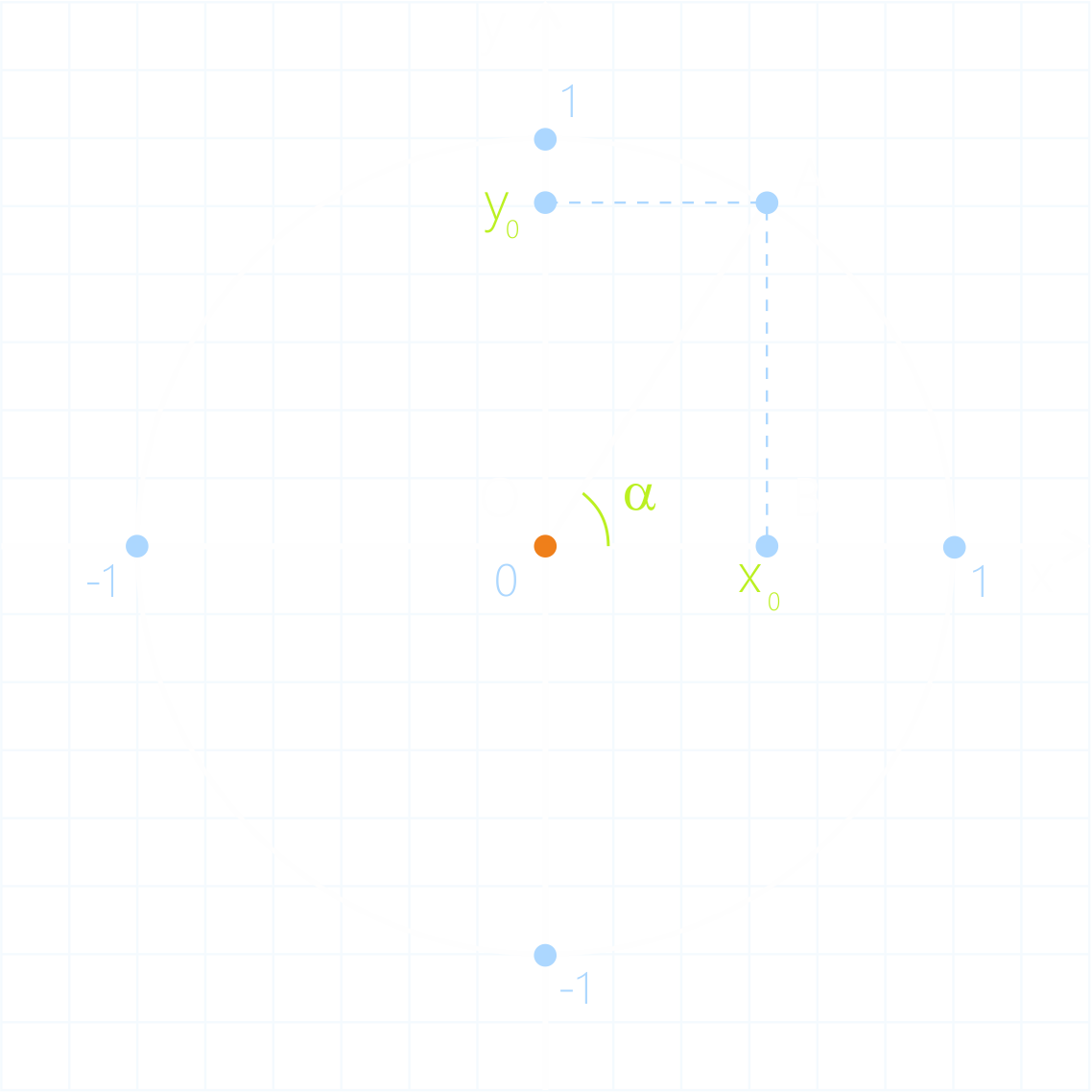
Единичный круг.
Отметим на оси х точку
x{|index|0|} и обозначим ее буквой В, а на оси у точку y{|index|0|} и
обозначим буквой А. Тогда sinα=AB, а cosα=OB.
Мы получили
прямоугольный треугольник АОВ, для которого справедливо равенство AB{|pow|2|}+OB{|pow|2|}=AO{|pow|2|}.
АО – радиус единичной
окружности, значит, АО=1.
Заменим в равенстве исходные данные и получим:
sin{|pow|2|}α+cos{|pow|2|}α=1, что и требовалось доказать.
Теперь Вы легко сможете вывести формулу нахождения синуса и косинуса.
Вот эти формулы:
cosα=±{|root|1-sin{|pow|2|}α|} и sinα=±{|root|1-cos{|pow|2|}α|}
Заключение
Вы познакомились с основным тригонометрическим
тождеством. Теперь при известном синусе Вы сможете быстро найти косинус угла и
наоборот. Эти знания пригодятся Вам в решении тригонометрических задач и при
сдаче ЕГЭ. Особенно внимательными нужно быть при выборе знака перед корнем. Для
этого достаточно вдумчиво читать условия. А теперь предлагаем потренироваться
применять основное тригонометрическое тождество в решении.
0

Аккаунт
Учёба
Статистика
