Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Синус угла
Вступление
Наше занятие сегодня будет посвящено изучению синуса. Как найти синус угла? Какие данные для этого понадобятся? Всё это мы сегодня изучим на примере прямоугольного треугольника. Кроме того, Вы узнаете, что существует таблица синусов. В ней собраны самые распространённые значения синусов углов, которые встречаются в задачах на тригонометрию. Для Вашего удобства углы будут указаны не только в градусах, но и в радианах. Постарайтесь запомнить, чему равны синусы углов, ведь знание этих значений существенно сократит время на решение тригонометрических задач.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Синус угла
Рассмотрим прямоугольный треугольник. Напомним, что стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая напротив прямого угла называется гипотенузой.
Синус угла - это отношение противолежащего катета к гипотенузе.
{|sin|α|}={|frac|АС|СB|}={|frac|DE|EB|}={|frac|FG|GB|}.
Обратите внимание, что значение синуса острого угла прямоугольного треугольника не зависит от размеров самого треугольника, оно зависит только от величины угла.
Значения синусов некоторых острых углов полезно помнить, чтобы быстро решать задачи по тригонометрии.
Также
синус можно определить по единичной
окружности - окружности с центром в начале координат и радиусом 1.
Синус угла α называется
ордината конечной точки поворота точки с координатами на угол α
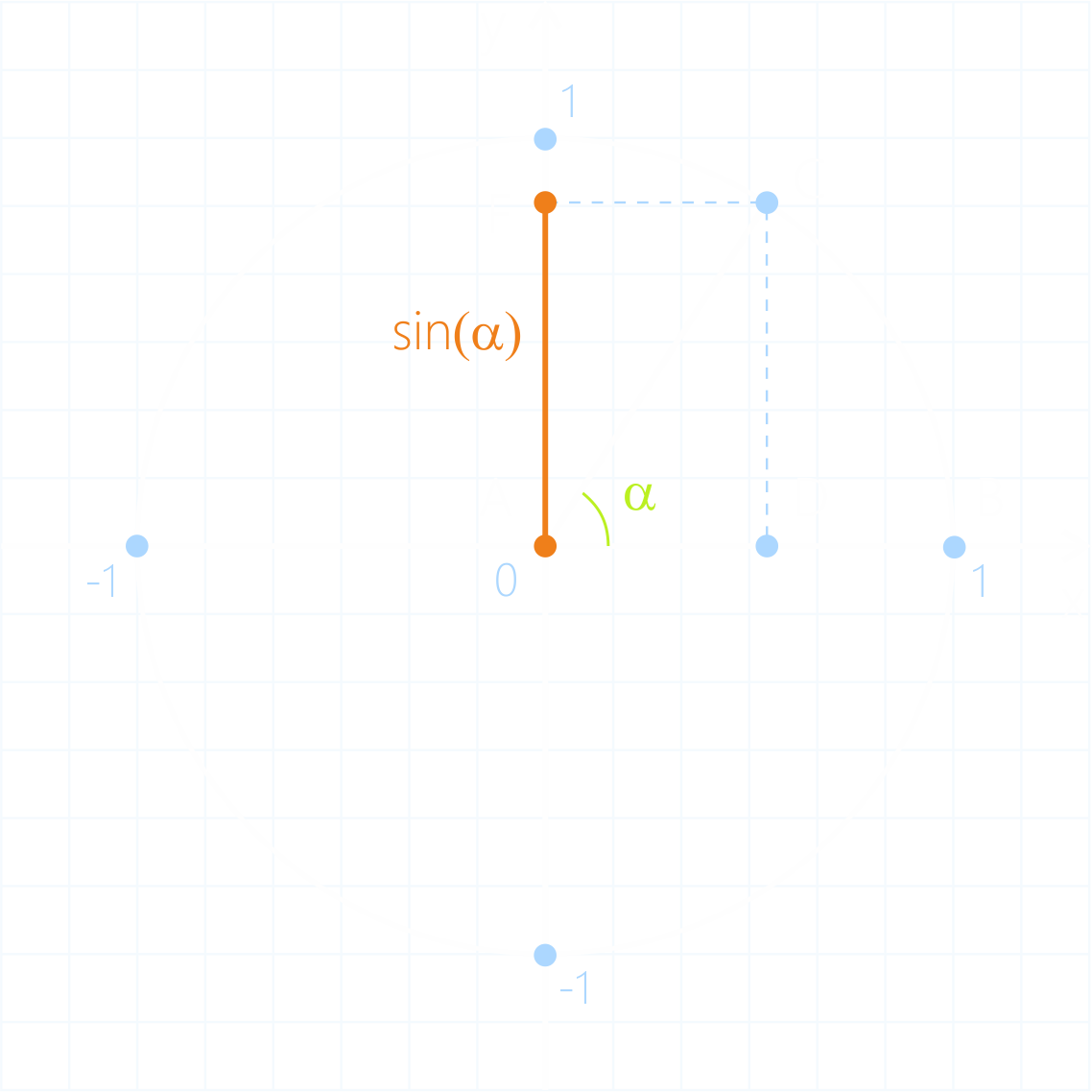
Определение синуса угла по единичной окружности
Заключение
Итак, мы с Вами изучили определение, что такое синус угла, узнали, как находить его значение, ознакомились с таблицей самых распространённых значений синусов углов, размер которых в таблице указан и в градусах, и в радианах. Осталось закрепить на практике пройденный материал. Виртуальный Учитель подготовил для Вас индивидуальные задания, решая которые Вы сможете потренироваться находить синус угла в треугольнике.
К вашей цели с Виртуальным учителем
