Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
Понятие многогранника
Вступление
Сегодня Вы начнёте знакомство с новым понятием, Вы узнаете, что такое многогранник. Вам будут представленны рисунки, чтобы Вы лучше представили себе, как он выглядит. Также Вы познакомитесь с частными случаями многоугольников, узнаете, что такое тетраэдр, октаэдр. Вы узнаете, что такое выпуклый и невыпуклый многогранник. Многогранники очень важны в стереометрии, это основные фигуры, поэтому Вы изучите их подробно.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Понятие многогранника
Многогранник - геометрическая фигура, состоящая из многоугольников и ограничивающая некоторую часть пространства.
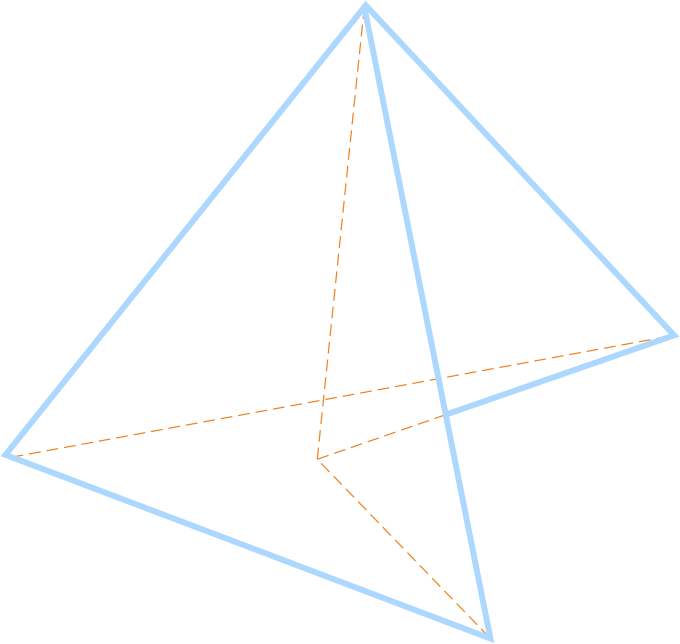
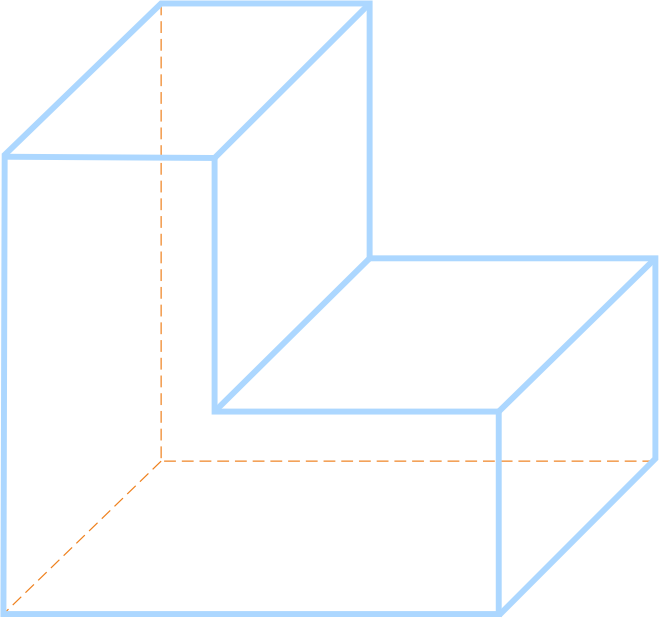
На рисунке изображены многогранники.
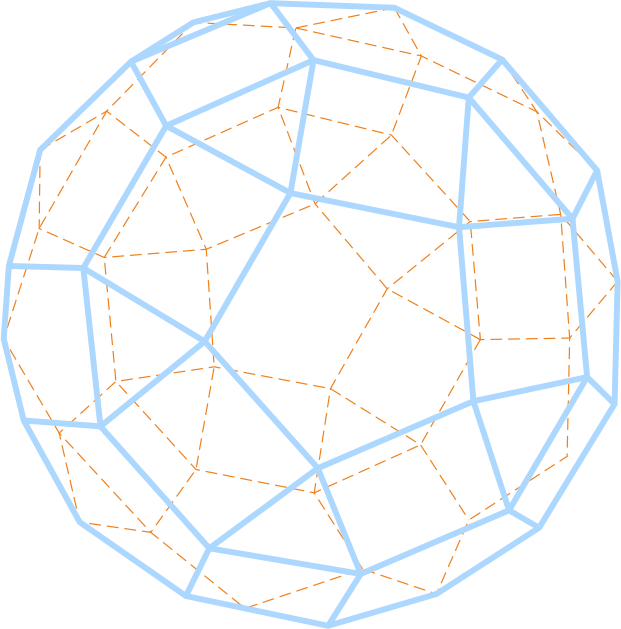
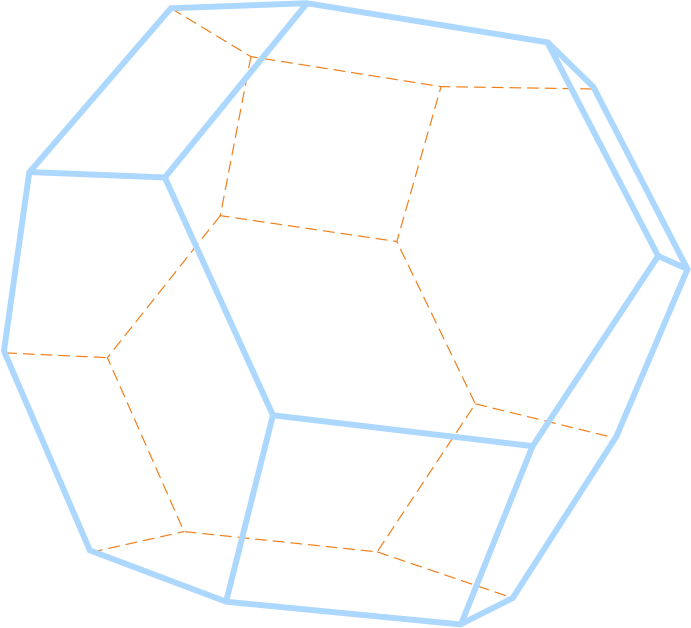

Рассмотрим примеры многогранников.
Тетраэдр - многогранник, состоящий из четырёх треугольников так, как показано на рисунке.
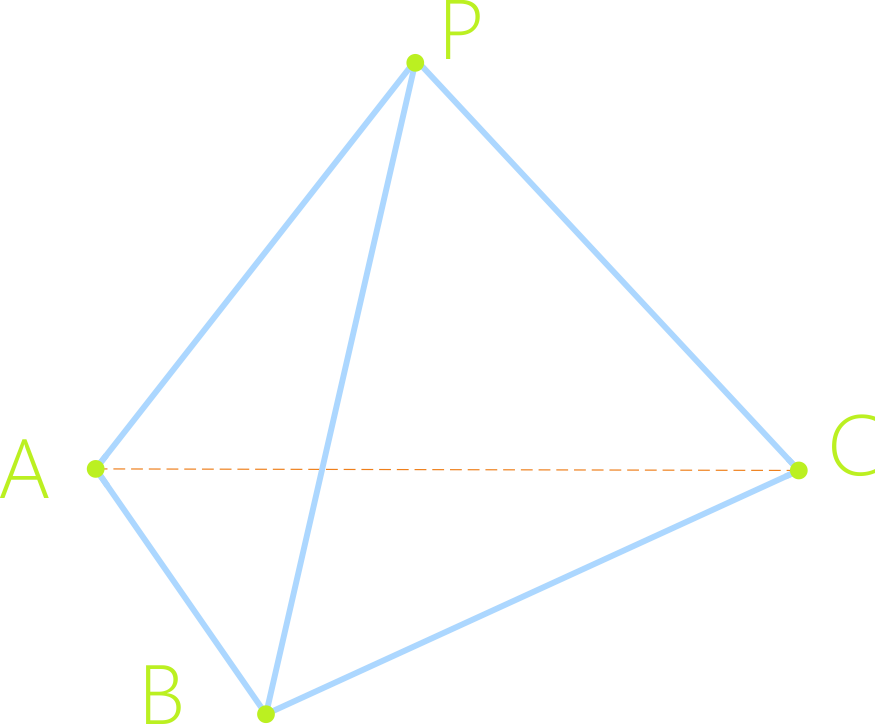
Октаэдр - многогранник, состоящий из восьми треугольников так, как показано на рисунке.
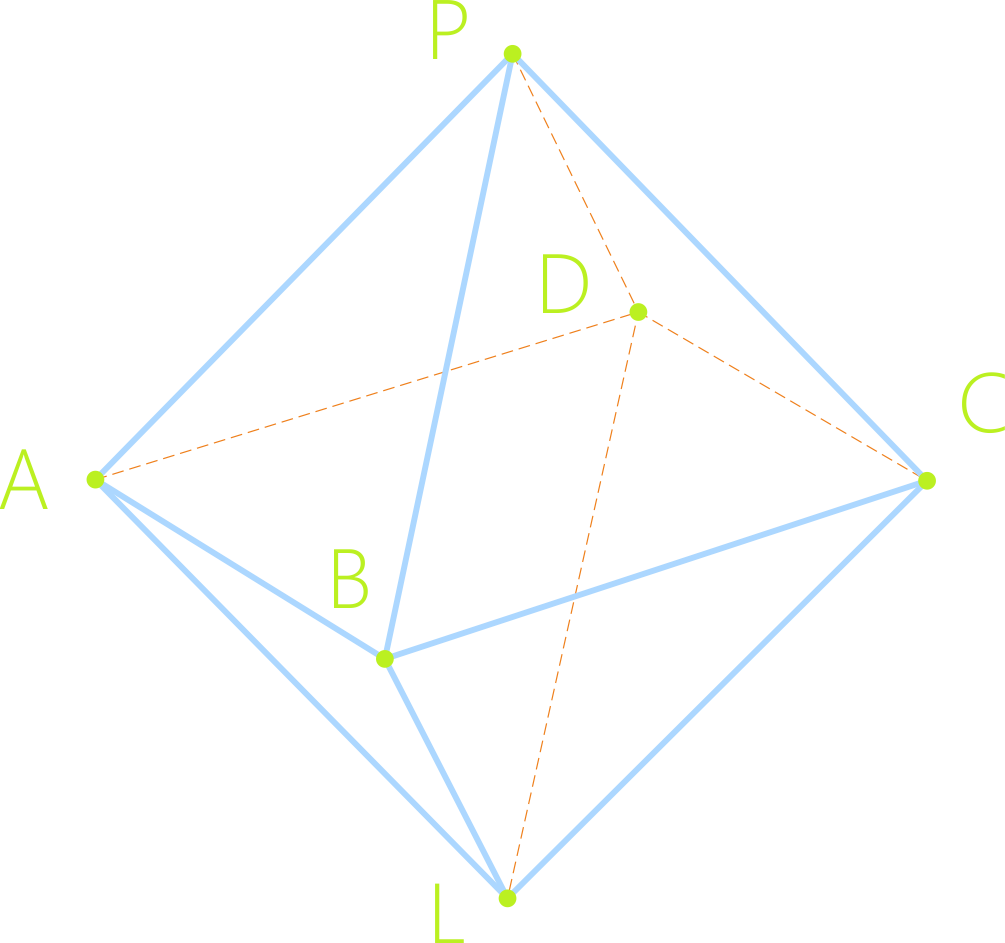
Выпуклый многогранник - многогранник, в котором сумма плоских углов при любой вершине меньше 360 градусов.
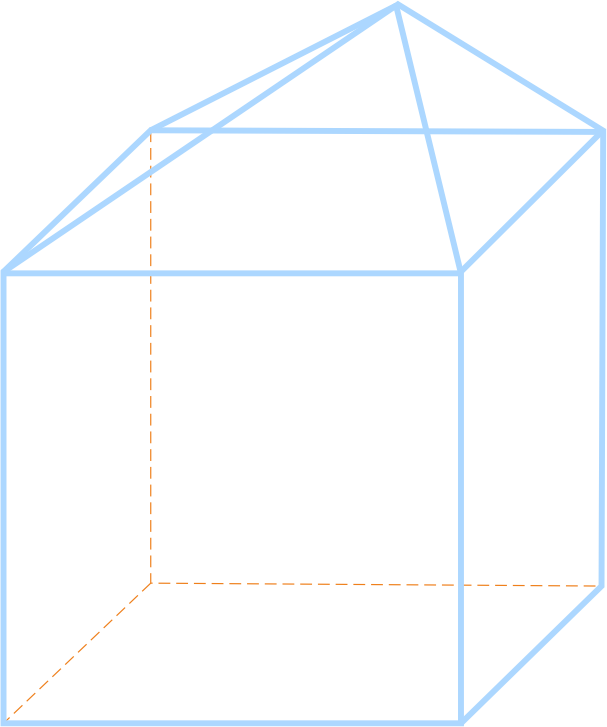
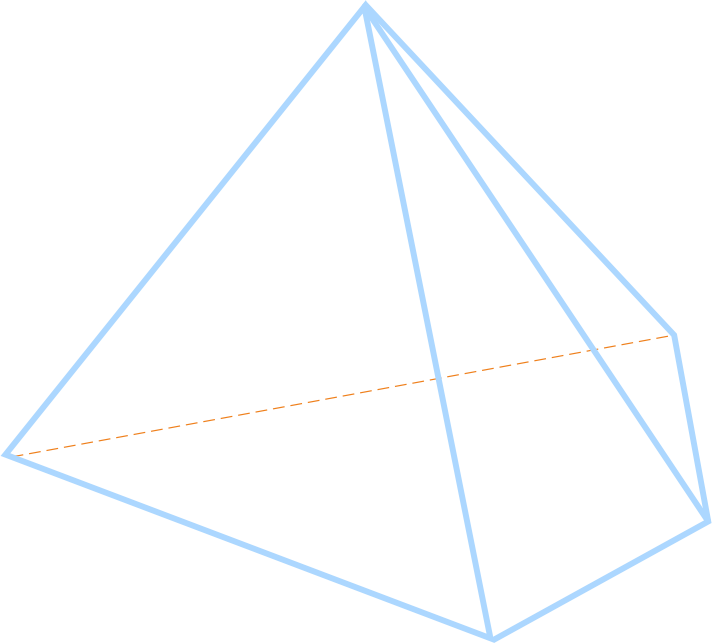
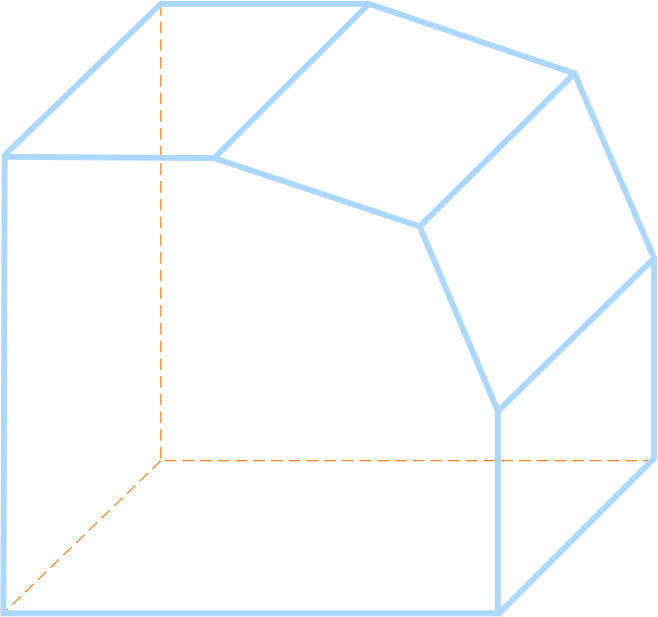
Невыпуклый многогранник - многогранник, в котором есть вершина, при которой сумма плоских углов не меньше 360 градусов.
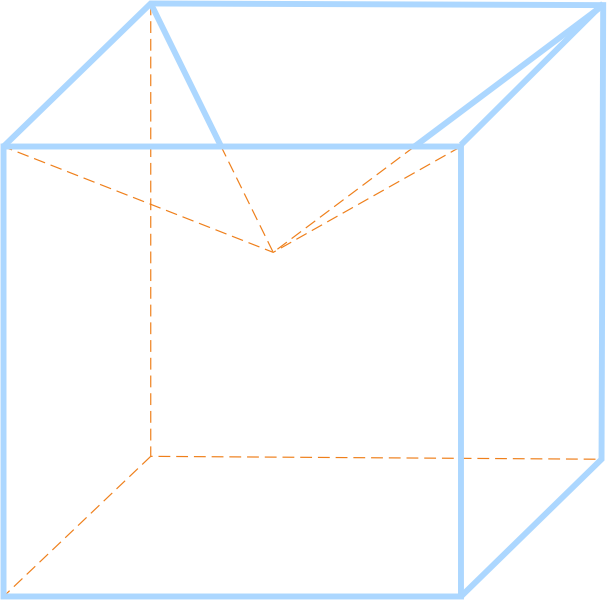
Заключение
Вы познакомились с понятием многогранника. На рисунках Вы смогли рассмотреть различные примеры многогранников. Вы узнали, что такое выпуклый и невыпуклый многогранник. Вы поняли, в чём между ними различие. Выпуклость - очень важное геометрическое понятие. Также Вы рассмотрели частные случаи многогранников - тетраэдр, октаэдр. Вы узнали, из чего эти фигуры состоят.
0

Аккаунт
Учёба
Статистика
