Правда ли, что математика – самый сложный предмет?Математика вызывает трудности у многих школьников. Но действительно ли её так трудно понять? Давайте разбираться вместе
Виртуальный
Учитель
Учитель
Взаимное расположение двух окружностей
Вступление
Вы уже
знаете уравнение окружности в координатах декартовой, прямоугольной плоскости.
И также знаете возможные расположения прямых на плоскости. Тема нашего занятия
совмещение двух вышеизложенных - взаимное расположение окружностей. Вы узнаете,
что такое касающиеся окружности, пересекающиеся окружности, а также когда одна
окружность лежит внутри другой. Приступим к изучению нового, полезного
материала об окружностях.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Взаимное расположение двух окружностей
Две окружности, расположенные на
плоскости, могут не касаться друг с другом. Две окружности могут иметь одну общую
точку, такие окружности называются касающимися. Также, две окружности могут
иметь две общие точки, такие окружности мы называем пересекающимися.
Рассмотрим с Вами все возможные
варианты взаимного расположения окружностей на плоскости.
R– радиус одной окружности. r– радиус второй окружности. d– расстояние между центрами окружностей.
d > R + r
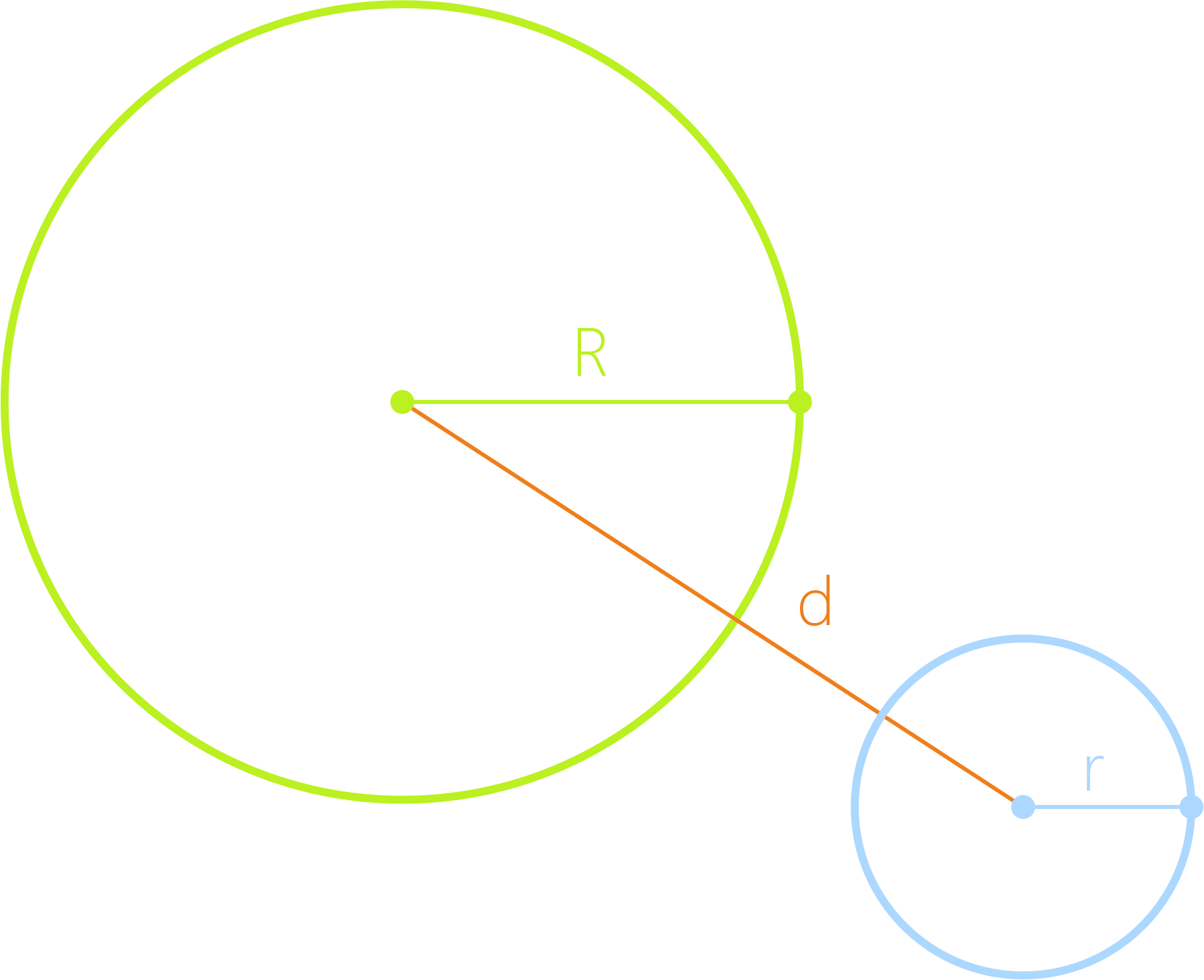
Не имют общих точек и не лежат одна в другой
d = R + r
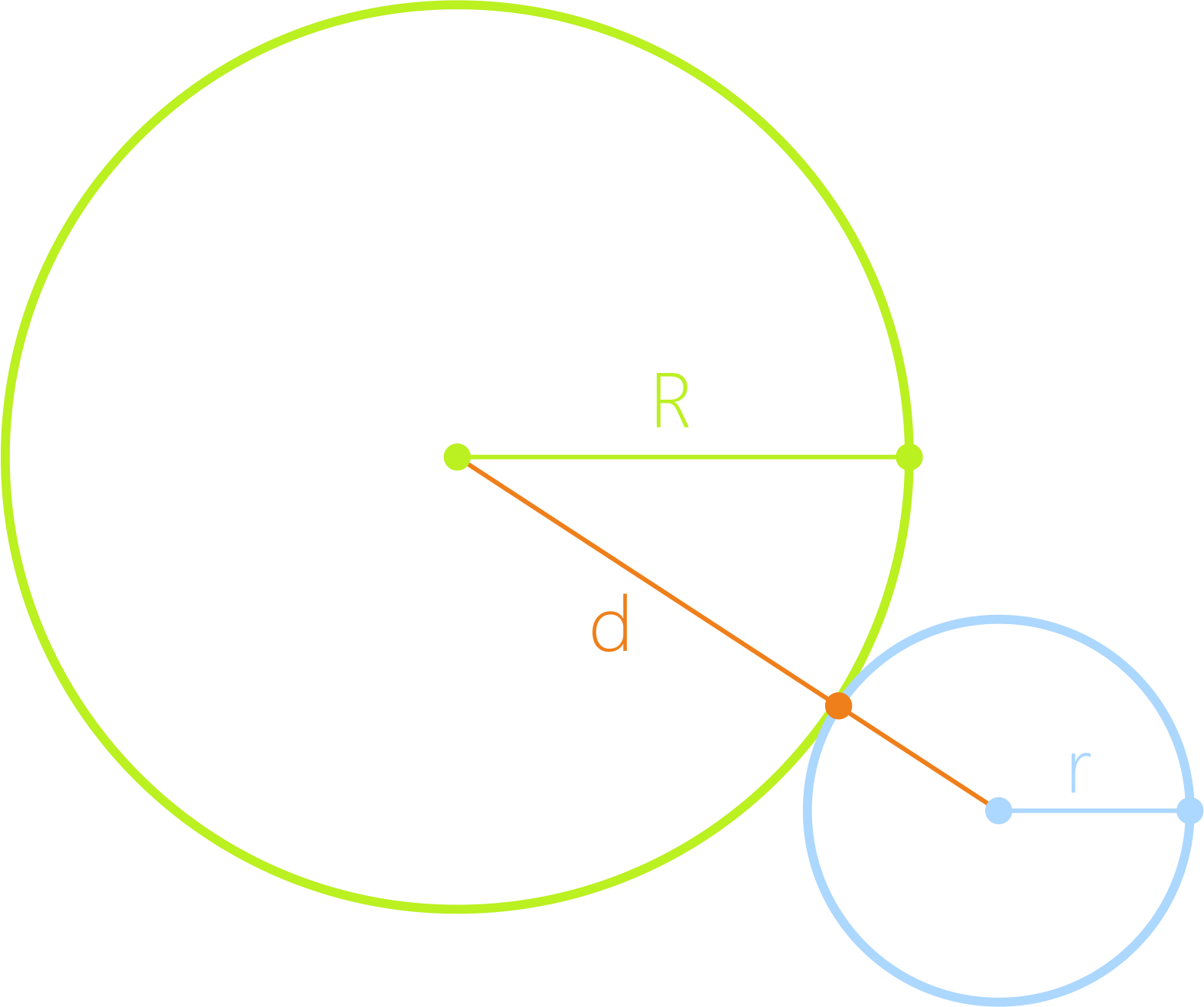
Имеют ровно одну общую точку и не лежать одна в другой. Другими словами, окружности касаются внешне, т.е. они касающиеся окружности
R -r < d < R + r
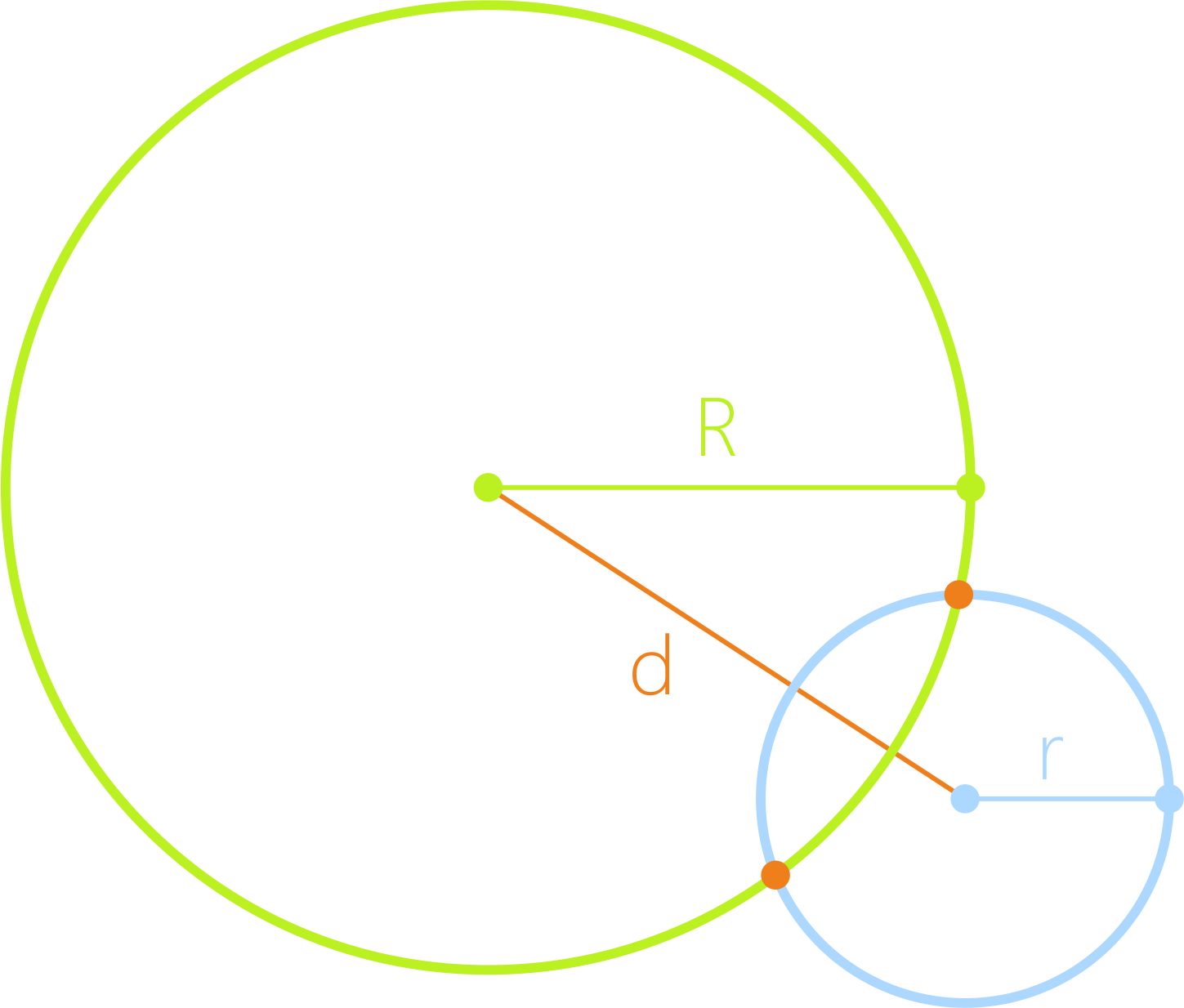
Имеют две точки пересечения, они называются пересекающиеся окружности
d = R
- r
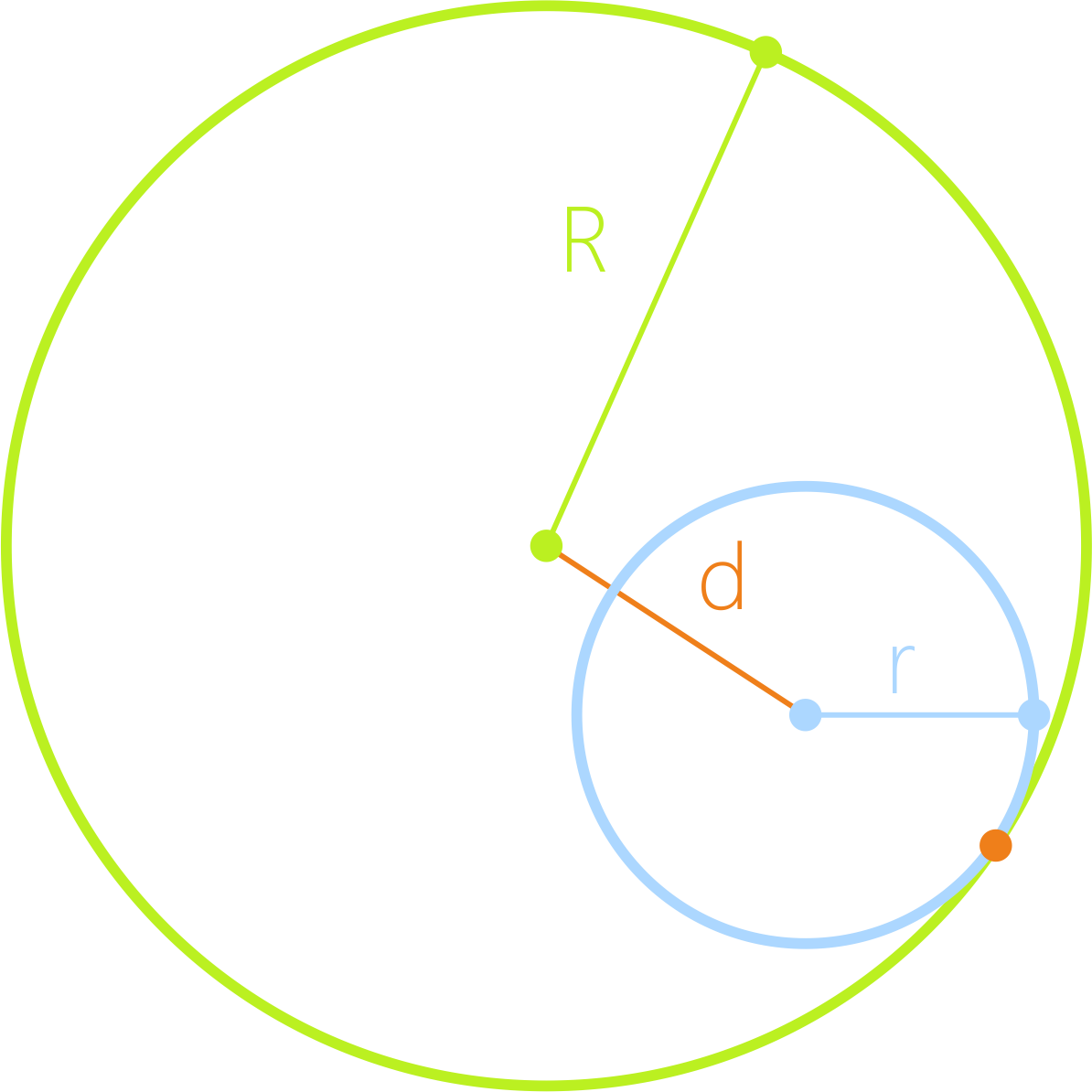
Имеют одну общую точку, но лежать одна в другой (окружности касаются внутренне, они касающиеся
окружности)
d <
R - r
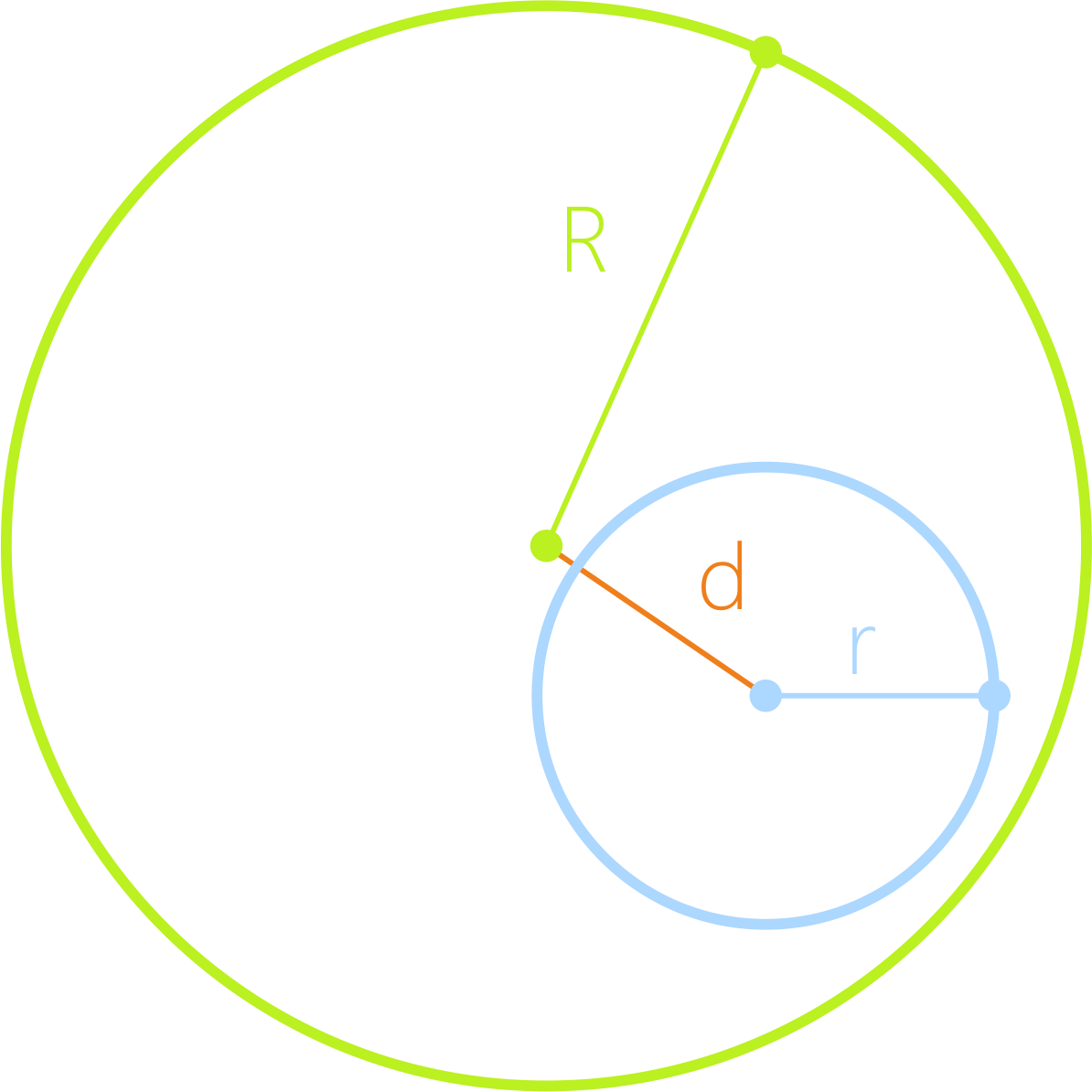
Не имеют общих
точек и одна лежит в другой
d = 0
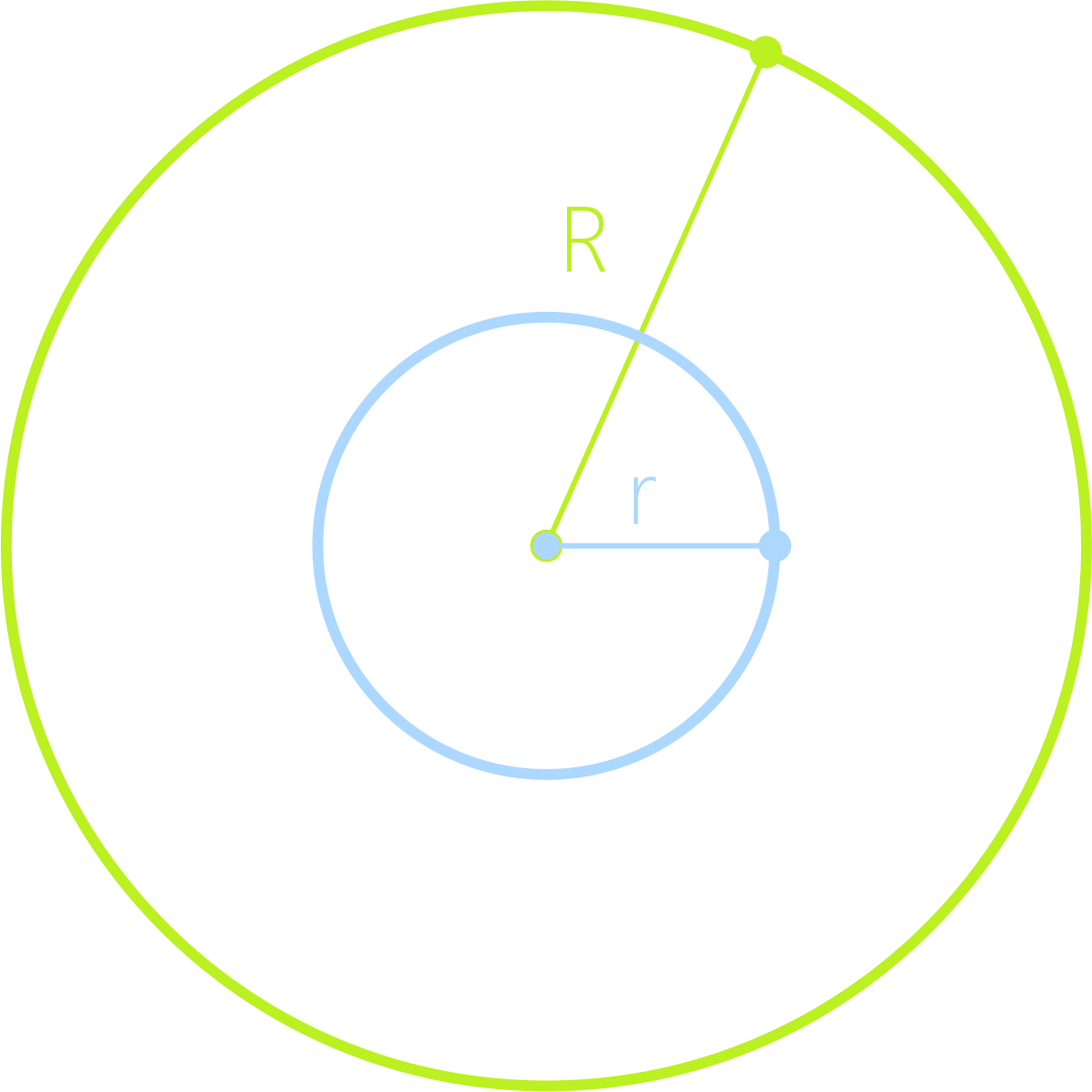
Центры окружностей совпадают
Заключение
Сегодня
Вы узнали взаимное расположение окружностей, Вы также познакомились с
уравнениями, которые и определяют расположение окружностей. Вы узнали новые
определения, в частности когда окружности касаются извне, что такое
пересекающиеся окружности и касающиеся окружности. Все полученные знания Вам
необходимы для решения задач на расположение окружностей и расстояния между
ними. Теперь для закрепления полученного материала Вы можете решить задачи по
этой теме, подготовленные для Вас.
0

Аккаунт
Учёба
Статистика
