Как преодолеть тревожность на экзамене?Как быть, если волнение или тревожность мешают Вам сосредоточиться? Несколько простых действий вернут Вас в состояние покоя. Читайте, что нужно делать, в нашей статье.
Виртуальный
Учитель
Учитель
Экстремум функции
Вступление
Изучая изображения графиков функций, Вы, скорее всего, заметили, что есть участки, на которых функция возрастает, есть участки, на которых функция убывает, а есть точки, в которых заданная функция достигает максимума или минимума. Что это за точки? Какое название они имеют? Как их находить? Сегодня мы найдём ответы на все эти вопросы. Давайте начинать.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Поиск точек экстремума функции
Понятие производной также полезно для нахождения точек экстремума функции.
Точки экстремума функции - это точки, в которых достигается локальный минимум или максимум функции.
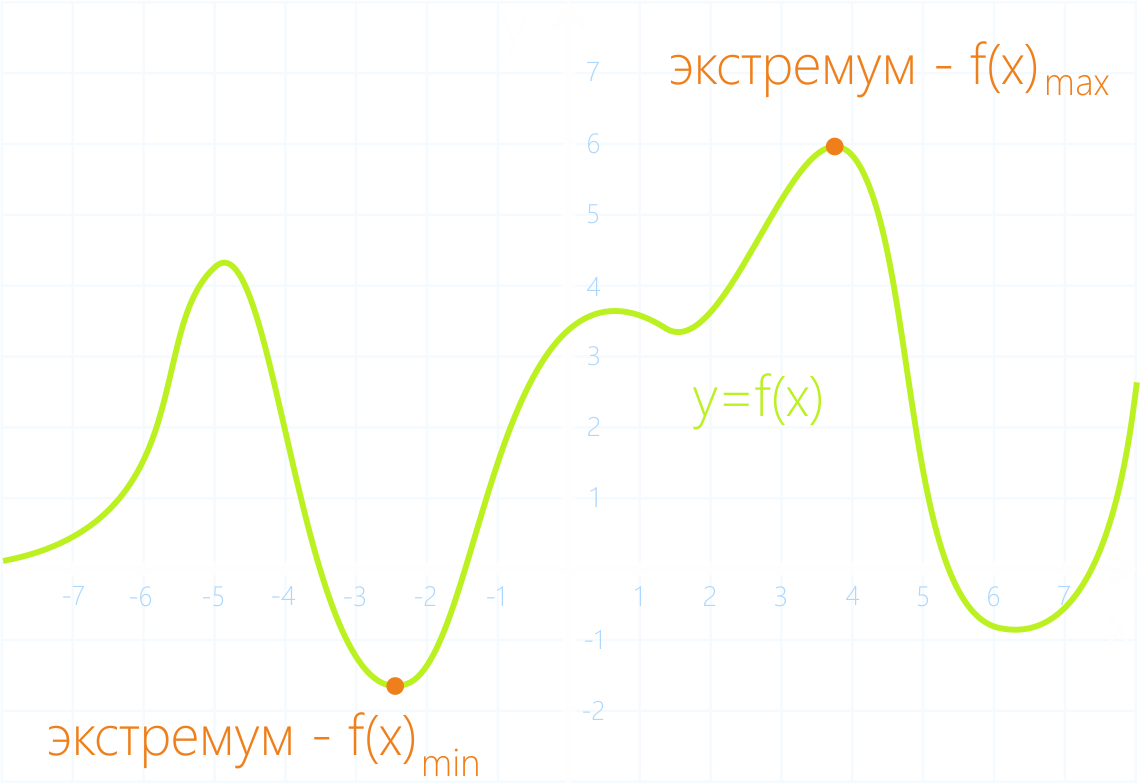
Теорема. Если функция y=f(x) имеет точки экстремума, то в этих точках производная функции либо равна нулю, либо не существует.
Чтобы найти точки экстремума функции y=f(x), необходимо:
- найти производную f?(x),
- найти все точки, в которых f?(x)=0,
- нарисовать числовую прямую и отметить найденные точки на ней,
- определить знак производной на каждом полученном промежутке прямой,
- если для какой-либо точки на прямой соседние интервалы имеют разный знак, значит такая точка является точкой экстремума функции.
Если производная функции в точке экстремума меняет знак:
- с отрицательного на положительный, то данная точка является точкой локального минимума функции,
- с положительного на отрицательный, то данная точка является точкой локального максимума функции.
Заключение
Наше сегодняшнее занятие было посвящено изучению алгоритма поиска точек экстремума функции. Для начала мы разобрались, что называют точками экстремума функции и узнали, что это точки локальных максимумов и локальных минимумов функции. Затем рассмотрели теорему и последовательность действий при поиске точек экстремума. После чего научились определять, чем является найденная точка экстремума локальным минимумом или локальным максимумом. Осталось лишь закрепить на практике пройденный материал. Для этого выполните задания от Виртуального Учителя.
К вашей цели с Виртуальным учителем
