Почему время учить математику именно в школе?Взрослые часто любят говорить: «Всему своё время.» А мы с уверенностью готовы утверждать, что лучшее время для изучения математики именно в школе!
Виртуальный
Учитель
Учитель
Формулы вычисления координат точки
Вступление
Вы знакомы с координатной плоскостью и знаете, как найти координату
любой точки. Но в геометрии существует и другой способ сделать это. Для
нахождения координаты по оси абсцисс и координаты по оси ординат существуют
универсальные формулы. Так можно найти координаты точки, если единичный отрезок
не задан. Задания такого рода встречаются во всех вариантах ОГЭ и ЕГЭ, поэтому
давайте приступим к изучению новой темы.
Какие темы нужно изучить, чтобы знать эту тему
Теория по теме Формулы вычисления координат точки
Рассмотрим прямоугольную систему координат Оху. Возьмём произвольную
точку А с координатами х; у. построим
единичную полуокружность.
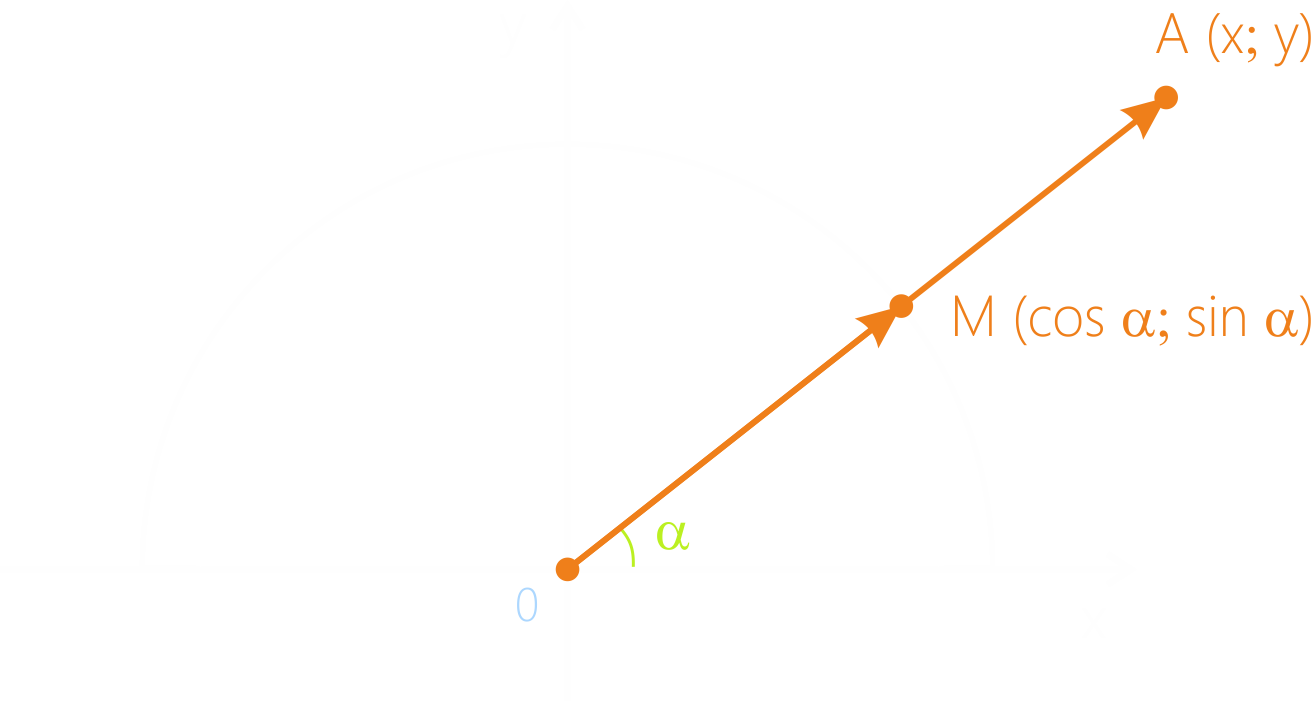
Теперь соединим начало координат с точкой А и получим
отрезок ОА, отрезок ОМ (точка М на пересечении с единичной полуокружностью),
угол α.
Вспомним, что координаты точки М – это {|cos|α|} (абсцисса), {|sin|α|} (ордината). Тогда координаты вектора будут соответственно {{|cos|α|};{|sin|α|}}.
Соответственно,
исходя из координат , получаем координаты вектора . Также . Из этого следует, что найти абсциссу точки А
можно так: OA*{|cos|α|}, ординату можно найти так: OA*{|sin|α|}.
Таким образом, получаем формулы нахождения
координат точки:
x=OA*{|cos|α|}
Заключение
Вы познакомились с формулами определения координат точки на плоскости.
Теперь Вы быстро сможете сделать это, если единичный отрезок не задан, но
известны другие данные. Для этого достаточно знать длину отрезка, соединяющего
начало координат и угол, который этот отрезок образует с осью абсцисс. Сейчас
Вы можете потренироваться находить координаты точки по выведенным формулам,
самостоятельно решать задачи и находить уогл α между осью х и лучом ОА при
известных координатах точки А.
0

Аккаунт
Учёба
Статистика
